Test de Shapiro-Wilk – Excel y Google Sheets
Este tutorial mostrará cómo realizar el Test de Shapiro-Wilk en Excel y Google Sheets.
El Test de Shapiro-Wilk es un test estadístico que se realiza para determinar si un conjunto de datos puede modelarse mediante la distribución normal y, por tanto, si puede decirse que un subconjunto del conjunto de datos seleccionado al azar está distribuido normalmente. La prueba de Shapiro-Wilk se considera uno de los mejores métodos numéricos de comprobación de la normalidad debido a su elevada potencia estadística.
La prueba original de Shapiro-Wilk, como la mayoría de las pruebas de significación, se ve afectada por el tamaño de la muestra y funciona mejor para tamaños de muestra de n=2 a n=50. Para tamaños de muestra mayores (hasta n=2000), puede utilizarse una extensión de la prueba de Shapiro-Wilk denominada Test de Shapiro-Wilk Royston.
Cómo Funciona el Test de Shapiro-Wilk
El Test de Shapiro-Wilk contrasta la hipótesis nula de que el conjunto de datos procede de una población con distribución normal con la hipótesis alternativa de que el conjunto de datos no procede de una población con distribución normal.
La estadística del test de Shapiro-Wilk es la siguiente: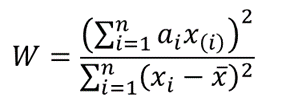 
donde x(i) es el estadístico de orden ith (es decir, el ith valor de los datos después de que el conjunto de datos está ordenado en orden ascendente),
es la media del conjunto de datos.
n es el número de puntos de datos del conjunto de datos, y
a = [ai] = (a1,…,an ) es el vector de coeficientes de las ponderaciones del test de Shapiro-Wilk (obtenido de la tabla de la prueba de Shapiro-Wilk),
El vector a es antisimétrico, es decir, a n+1-i =-ai para todos los i, y a(n+1)/2 = 0 para los n impares. Also, aT a = 1
El valor p se obtiene comparando el estadístico W con los valores W presentados en la tabla de valores p del test de Shapiro-Wilk para el tamaño de muestra dado.
- Si el valor – obtenido es inferior al nivel de significación elegido, se rechaza la hipótesis nula y se concluye que el conjunto de datos no procede de una población con distribución normal,
- En caso contrario, no se rechaza la hipótesis nula y se concluye que no hay pruebas estadísticamente significativas de que el conjunto de datos no proceda de una población con distribución normal.
Cómo Realizar la Prueba de Shapiro-Wilk en Excel
Antecedentes: En la siguiente tabla se presenta una muestra de las estaturas, en pulgadas, de 14 niños de diez años. Utilice el método Shapiro-Wilk de comprobación de la normalidad para probar si los datos obtenidos de la muestra pueden modelarse utilizando una distribución normal.
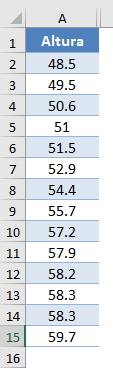
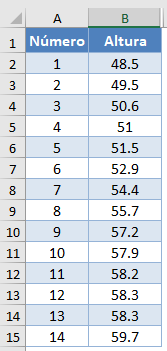
En primer lugar, seleccione los valores del conjunto de datos y ordene los datos con la herramienta Ordenar: Datos > Ordenar (Ordenar de menor a mayor)
Esto ordenará los valores de la siguiente manera
Alternativamente, con las nuevas versiones de Excel, puede utilizar la función ORDENAR para ordenar los datos:
=ORDENAR(B2:B15)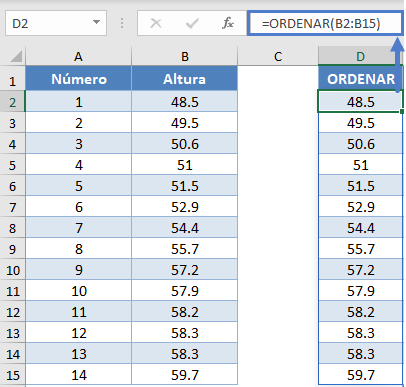
A continuación, calcula el denominador del estadístico W, 
, como se muestra en la imagen siguiente, utilizando PROMEDIO para calcular la media:
=(B2-PROMEDIO($B$2:$B$15))^2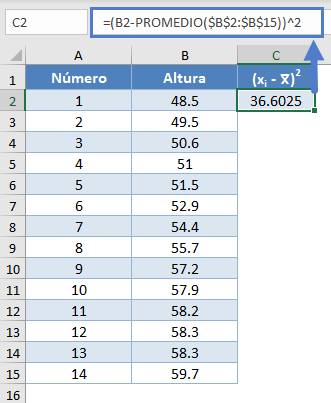
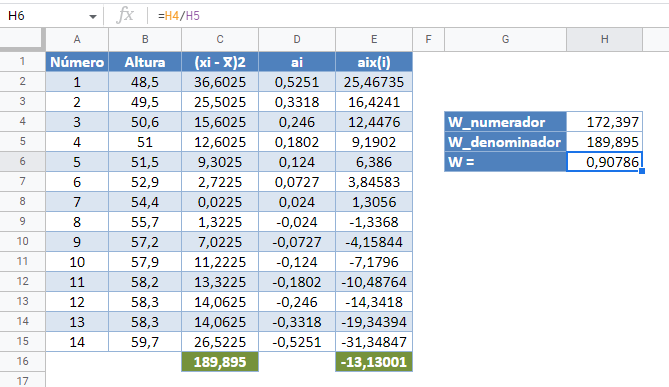
Completa el resto de la columna y luego calcula la suma (mostrada en el fondo verde) como se muestra en la siguiente imagen:
=SUMA(C2:C15)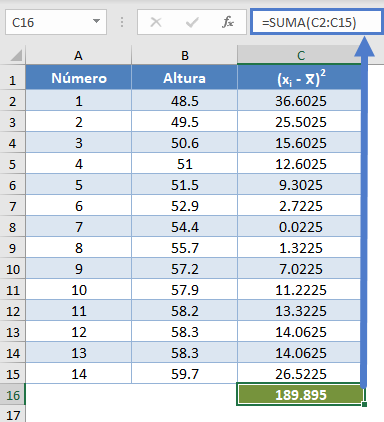
Así, el denominador de la estadística W es 189,895.
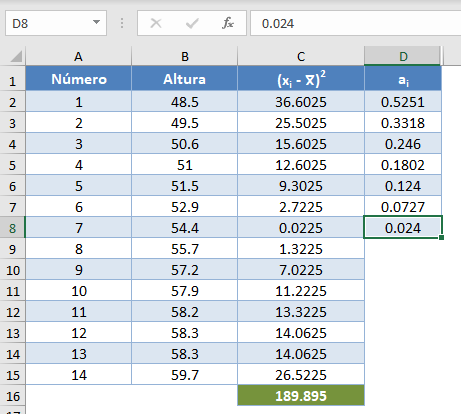
A continuación, obtenga los valores de ai, los coeficientes de los pesos de la prueba de Shapiro-Wilk, para un tamaño de muestra de n=14 a partir de la tabla de la prueba de Shapiro-Wilk. A continuación se muestra un extracto de la tabla del Test de Shapiro-Wilk: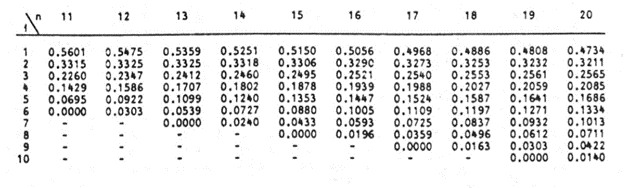 
Estos valores tendrán que ser introducidos manualmente de la siguiente manera:
Y utilizando la propiedad antisimétrica de ai, es decir, an+1-i=-ai para todo i, tenemos que a14=-a1, a13=-a2, etc. Por lo tanto, los valores completos de la columna ai se muestran en la siguiente imagen:
=-D8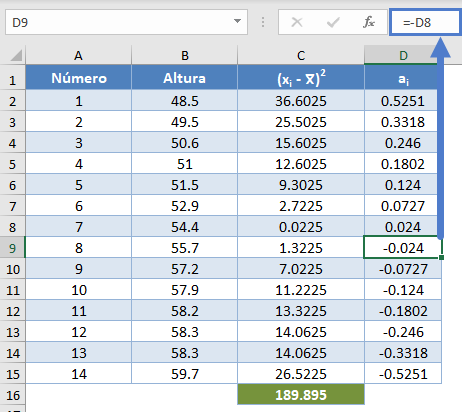
*Obsérvese que, debido a la propiedad antisimétrica de ai y a que el numerador del estadístico W es un cuadrado, no importa qué mitad de la columna ai es positiva o negativa. Es decir, puede elegir que la mitad superior de la columna sea positiva y la mitad inferior negativa o viceversa y no afectará a su resultado final.
A continuación, multiplique los valores de ai por los valores correspondientes (ya ordenados) en el conjunto de datos para obtener la columna aix(i). El cálculo y el valor para el primer punto de datos se muestran en la siguiente imagen:
=D2*B2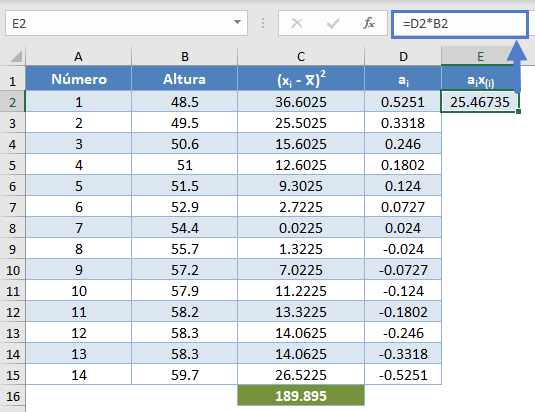
Complete el resto de la columna aix (i) y calcule la suma (mostrada en fondo verde) como se muestra en la imagen siguiente
=SUMA(E2:E15)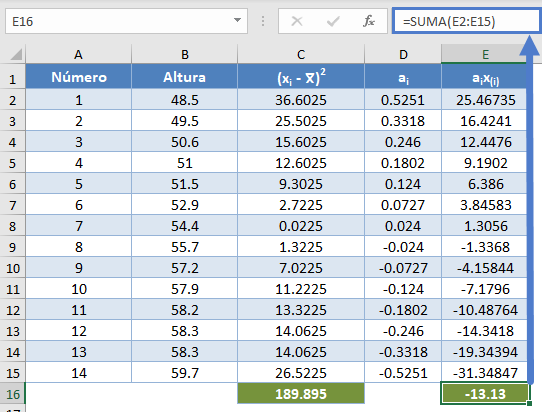
El denominador del estadístico W obtenido anteriormente es 189,895 , y el numerador es el cuadrado de la suma de la columna ai x(i). Por lo tanto, tenemos lo siguiente
=E16^2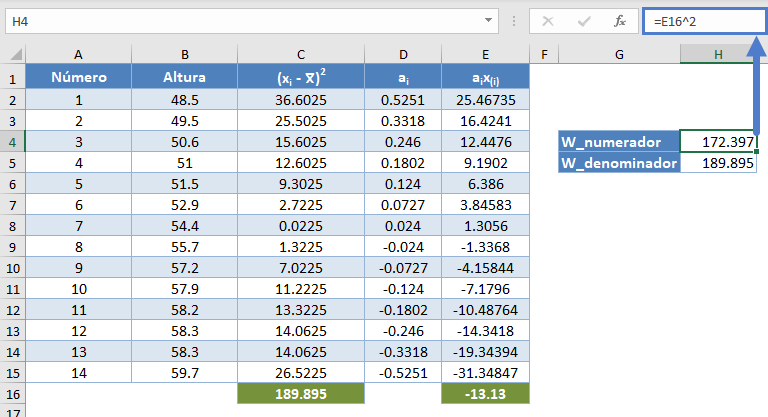
Por lo tanto, el estadístico W es el siguiente
=H4/H5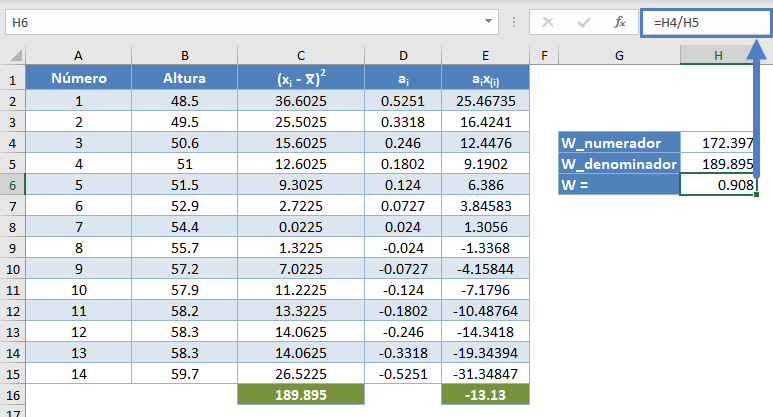
Por último, obtenga el valor p de la prueba utilizando la tabla de valores p de la prueba de Shapiro-Wilk teniendo en cuenta el tamaño de la muestra.
A continuación se muestra un extracto de la tabla de valores p de la prueba de Shapiro-Wilk: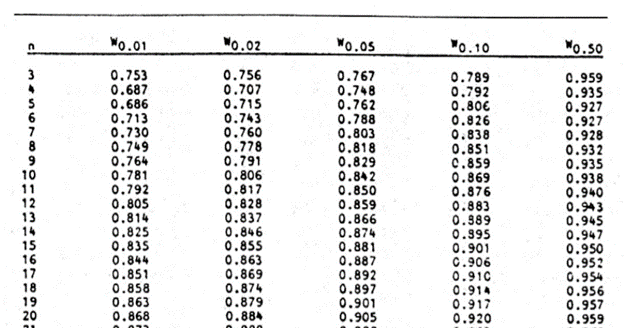 
Para esta prueba, utilizaremos un nivel de significación (alfa) de 0,05. En la tabla se puede ver que para n =14, W = 0,90786 está entre W0,10 = 0,895 y W0.50 = 0,947, lo que significa que el valor p está entre 0,10 y 0,50. Esto significa que el valor p es mayor que α = 0,05, por lo que no se rechaza la hipótesis nula.
Por lo tanto, concluimos que no hay pruebas suficientes de que el conjunto de datos no proceda de una población con distribución normal. Es decir, podemos suponer que el conjunto de datos está distribuido normalmente.
*Utilizando la interpolación lineal, se puede obtener que el valor p aproximado es de 0,1989.
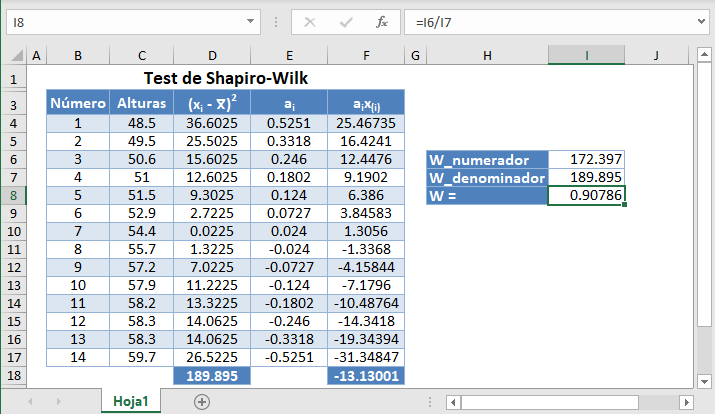
Test de Shapiro-Wilk en Google Sheets
El Test de Shapiro-Wilk se puede realizar en Google Sheets de forma similar a como se hace en Excel, tal y como se muestra en la siguiente imagen.
