Prueba de Suma de Rangos de Wilcoxon (Prueba U de Mann Whitney) – Excel y Google Sheets
Este tutorial demostrará cómo utilizar la Prueba de Suma de Rangos de Wilcoxon (Prueba U de Mann Whitney) en Excel y Google Sheets.
Comparar la Prueba T Independiente de Dos Muestras y la Prueba de Suma de Rangos de Wilcoxon
- Tanto la prueba T independiente de dos muestras como la prueba de suma de rangos de Wilcoxon se utilizan para determinar si existe una diferencia estadísticamente significativa entre DOS conjuntos de muestras independientes.
- La prueba T independiente de dos muestras supone que el conjunto de datos procede de una población con distribución normal, pero la prueba de suma de rangos de Wilcoxon no hace esta suposición.
Cuándo Utilizar la Prueba de Rango con Signo de Wilcoxon
La prueba de rango de Wilcoxon se utiliza cuando alguno de los conjuntos de datos viola la condición de normalidad y los dos conjuntos de muestras son independientes.
Supuestos para la Prueba de Suma de Rangos de Wilcoxon
- Los datos que se miden deben estar en el nivel ordinal o continuo. (Es decir, los datos deben ser una escala clasificada o un número)
- Las observaciones de ambas muestras son independientes entre sí.
Cómo Realizar la Prueba de Suma de Rangos de Wilcoxon en Excel
Tabla de Valores Críticos de la Prueba de Suma de Rangos de Wilcoxon
En este método, comparamos el estadístico de la prueba de suma de rangos de Wilcoxon con el valor crítico. A continuación se muestra la guía paso a paso sobre cómo realizar la prueba de suma de rangos de Wilcoxon utilizando el método de los valores críticos.
Ejemplo
Antecedentes: Se ha producido un nuevo fármaco para el tratamiento de los dolores de cabeza y las molestias. El fabricante afirma que el fármaco alivia los dolores de cabeza más rápidamente que los fármacos actuales del mercado. Un investigador quiere poner a prueba esta afirmación, por lo que colocó al azar a pacientes con fuertes dolores de cabeza en dos grupos. Administra el nuevo fármaco a uno de los grupos y uno de los populares fármacos más antiguos al otro grupo y registra el tiempo, en minutos, que tarda cada persona en sentir alivio del dolor de cabeza. El resultado se presenta en la siguiente tabla. Pruebe a un nivel de significación del 5% si existe una diferencia significativa en el tiempo que tardan el nuevo medicamento y el antiguo en aliviar el dolor de cabeza.
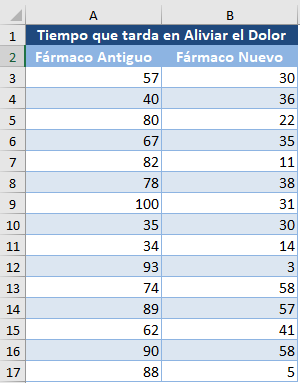
En primer lugar, asigne el rango a cada punto de datos (Tiempo) del más pequeño al más grande utilizando la función JERARQUIA.MEDIA:
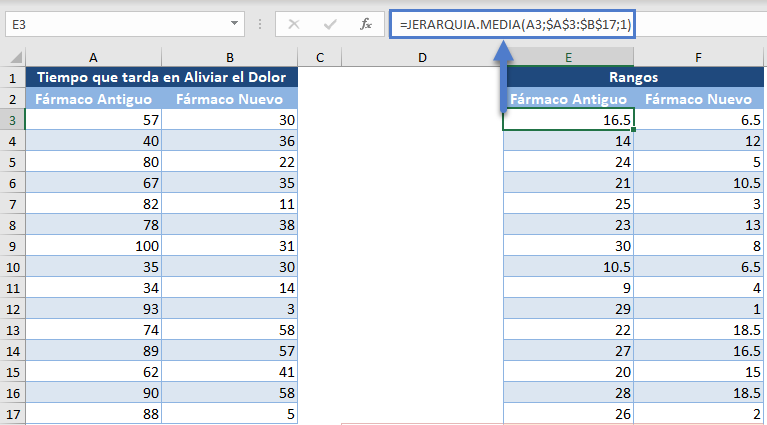
Tenga en cuenta que utilizamos referencias absolutas para el rango en la Función JERARQUIA.MEDIA para que podamos pegar fácilmente la fórmula a otras celdas sin cambiar el rango.
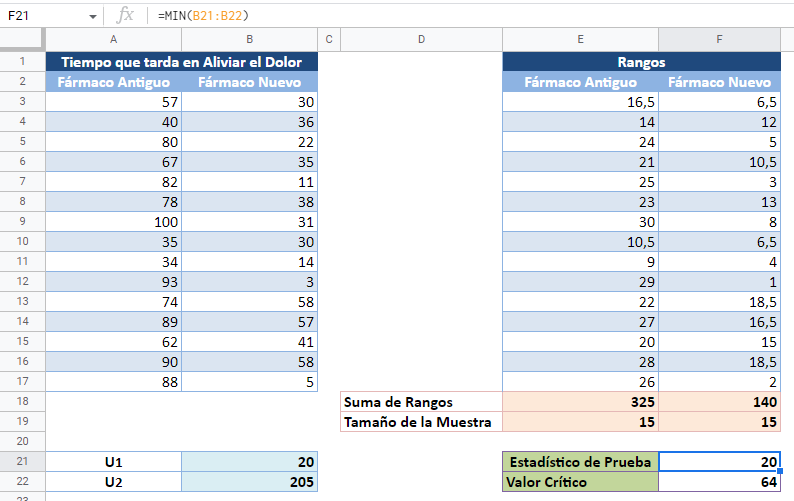
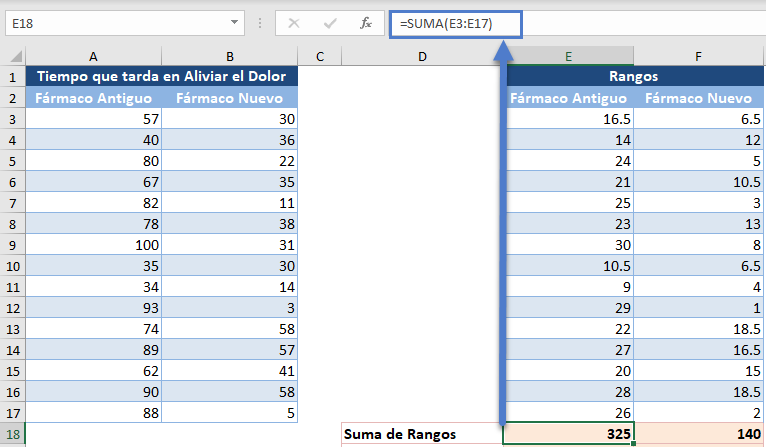
A continuación, obtenemos la suma de los rangos de cada grupo (el grupo de medicamentos antiguos y el grupo de medicamentos nuevos).
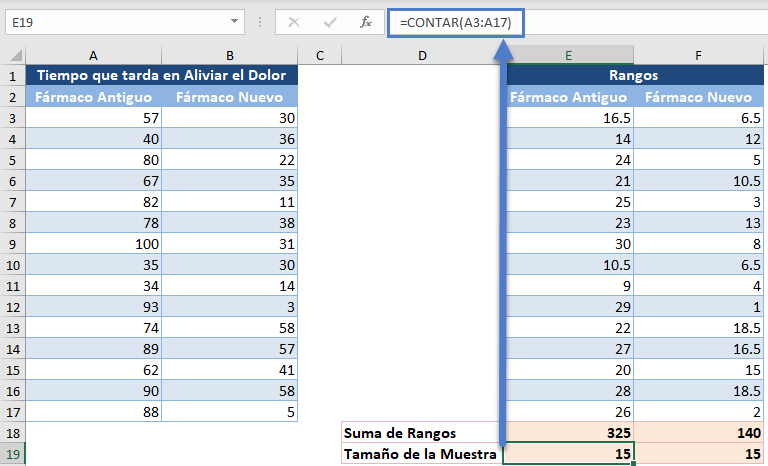
A continuación, utilice la función CONTAR para obtener los tamaños de las muestras de los dos grupos, como se muestra a continuación:
El estadístico de prueba para la prueba de suma de rangos de Wilcoxon se denota por U y es el menor de U1 y U2 definido por: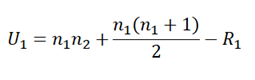 
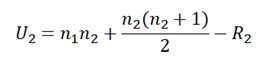Donde n1 y n2 son los tamaños de las muestras del grupo 1 (grupo de fármacos antiguos) y del grupo 2 (grupo de fármacos nuevos) respectivamente, y R1 y R2 son las sumas de los rangos del grupo 1 y del grupo 2 respectivamente.
A continuación, calculamos U1 y U2 como sigue:
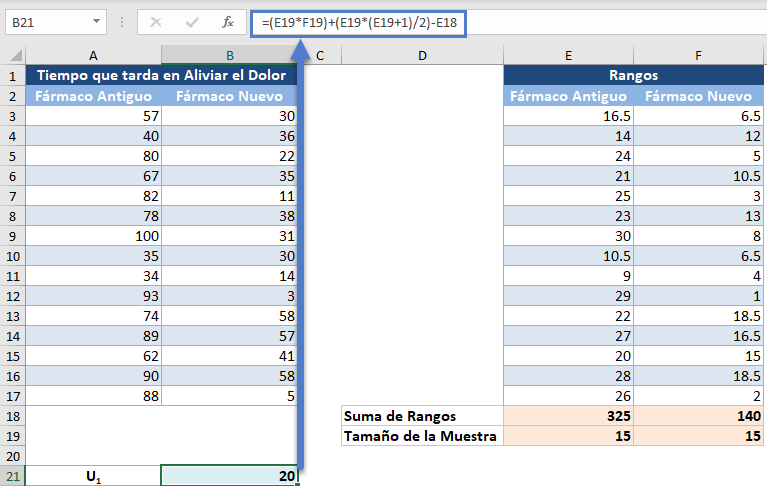
Del mismo modo, para U2:
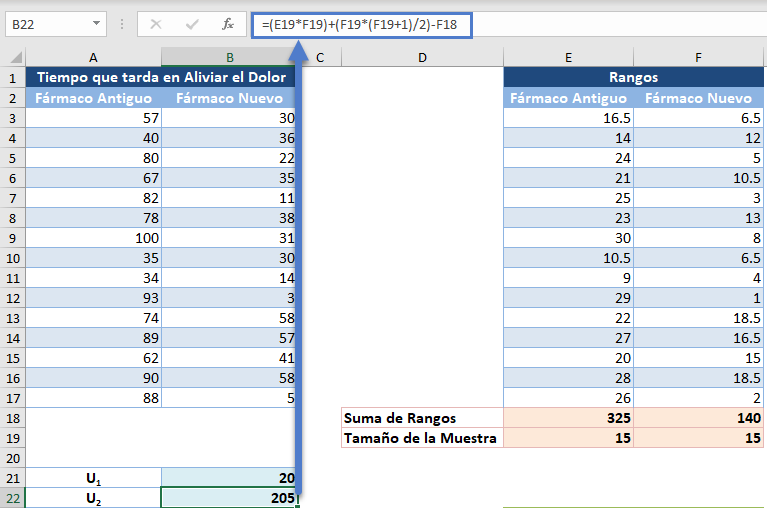
El estadístico de la prueba U, es el menor de U1 y U2 y se calcula como sigue:
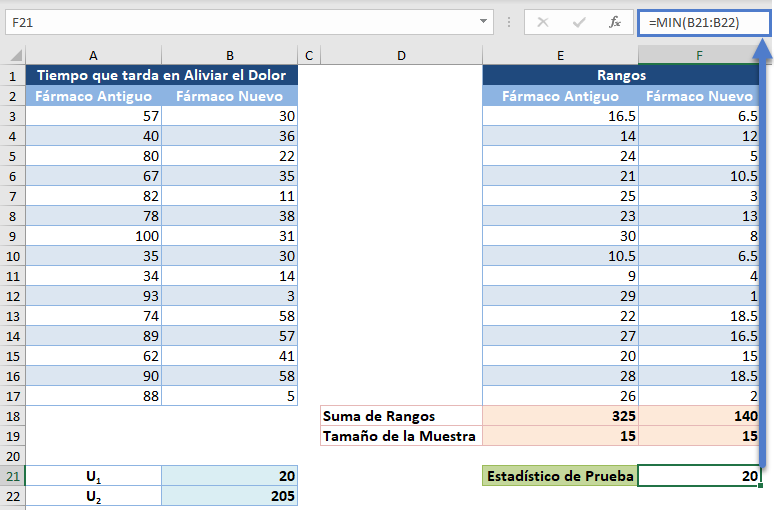
Ahora, obtenga el valor crítico para el tamaño de la muestra de n1= 15, n2 =15 y un nivel de significación del 5% a partir de la tabla de valores críticos de suma de Rangos de Wilcoxon.
Tenga en cuenta que estamos haciendo una prueba de dos colas aquí porque estamos probando la diferencia en los valores (y no el aumento o la disminución de los valores) que es en ambos sentidos, tanto el aumento como la disminución de los valores.
A continuación se muestra un extracto de la tabla de valores críticos de la pruba de suma de rangos de Wilcoxon (Prueba U de Mann-Whitney) para una prueba de dos colas:
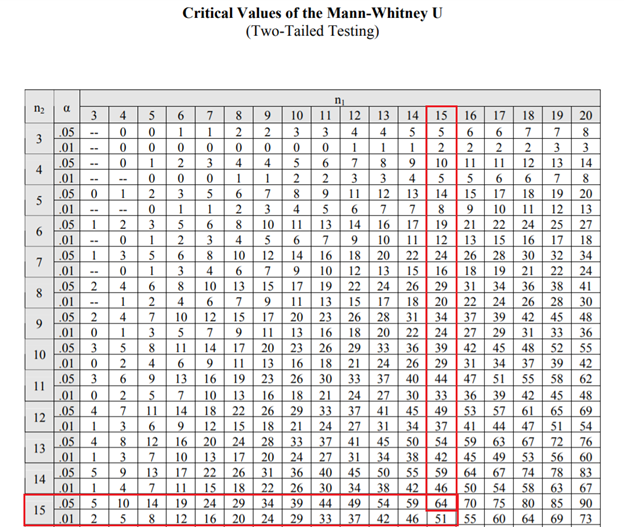
Por lo tanto, el valor crítico es 64.
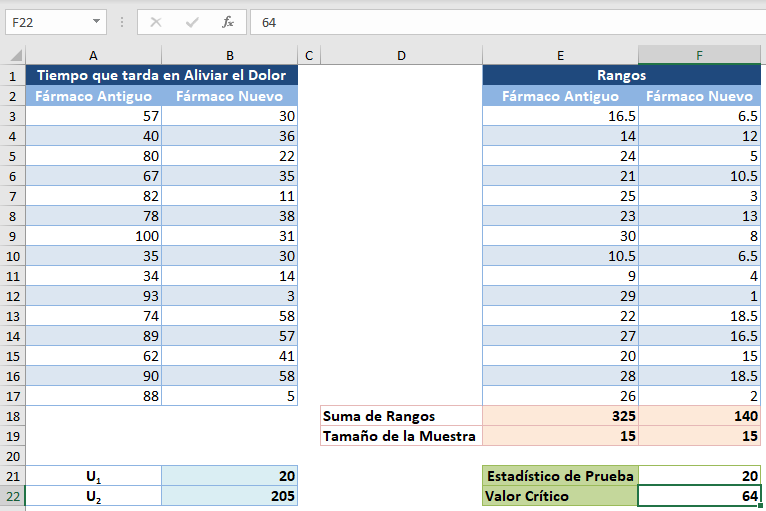
En el caso de la prueba de suma de rangos de Wilcoxon, concluimos que existe una diferencia significativa entre los grupos cuando la estadística de la prueba es menor o igual que el valor crítico.
En este caso, el estadístico de prueba es 20 y el valor crítico es 64, puesto que el estadístico de prueba es menor que el valor crítico, concluimos que hay pruebas estadísticamente significativas de que el nuevo medicamento alivia los dolores de cabeza más rápidamente que el antiguo.
Método del Valor p
Otro método para realizar la prueba de suma de rangos de Wilcoxon es aproximar la distribución a una distribución normal y luego usar el valor p de la puntuación z aproximada para hacer una conclusión sobre la población de los grupos.
En los siguientes pasos, ilustramos este método usando el mismo ejemplo utilizado en el método anterior.
Ejemplo
Antecedentes: Se ha producido un nuevo fármaco para el tratamiento de los dolores de cabeza y las molestias. El fabricante afirma que el fármaco alivia los dolores de cabeza más rápidamente que los fármacos actuales del mercado. Un investigador quiere poner a prueba esta afirmación, por lo que colocó al azar a pacientes con fuertes dolores de cabeza en dos grupos. Administra el nuevo fármaco a uno de los grupos y uno de los populares fármacos más antiguos al otro grupo y registra el tiempo, en minutos, que tarda cada persona en sentir alivio del dolor de cabeza. El resultado se presenta en la siguiente tabla. Comprueba a un nivel de significación del 5% si existe una diferencia significativa en el tiempo que tardan el nuevo medicamento y el antiguo en aliviar el dolor de cabeza.
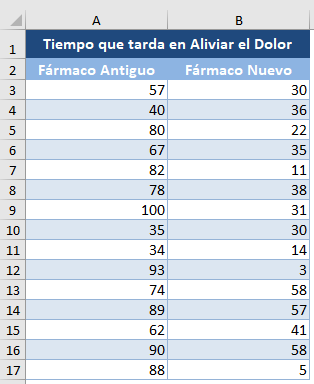
Vamos a seguir todos los pasos descritos en el método anterior para obtener la suma de los rangos de los dos grupos y los tamaños de las muestras.
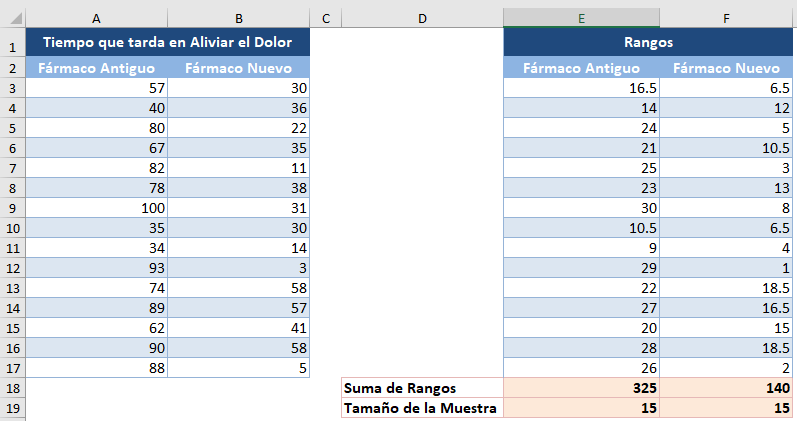
Para este método, el estadístico de prueba, T, es el menor de la suma de los rangos de los dos grupos, que se obtiene de la siguiente manera:
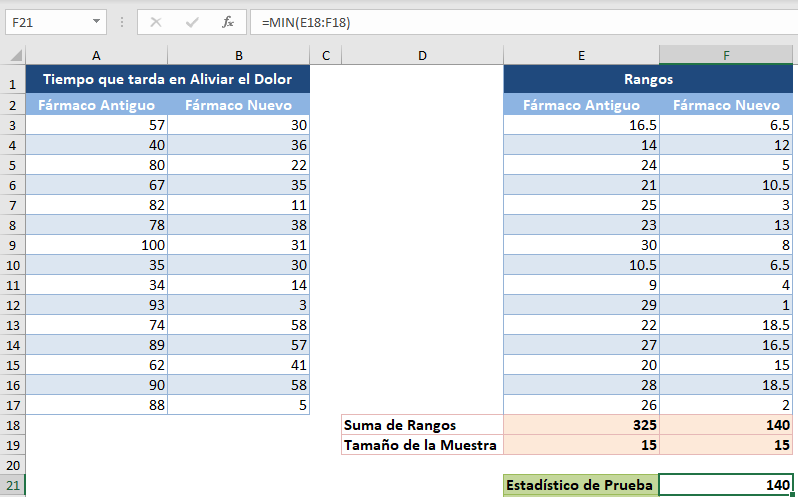
Ahora, obtendremos la media y el error estándar de la distribución. La media (μ) de la distribución viene dada por:
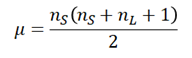
donde nS y nL son los tamaños de las muestras de los grupos de menor y mayor rango respectivamente, y el error estándar viene dado por: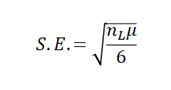 
que equivale a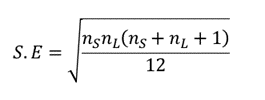 
Para nuestro caso, nS = nL= 15. Entonces, calculamos la media de la siguiente manera:
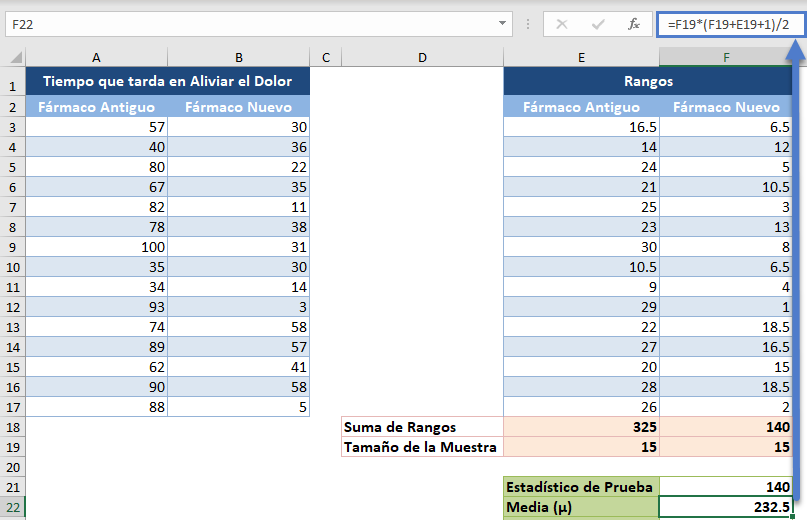
y el error estándar como sigue
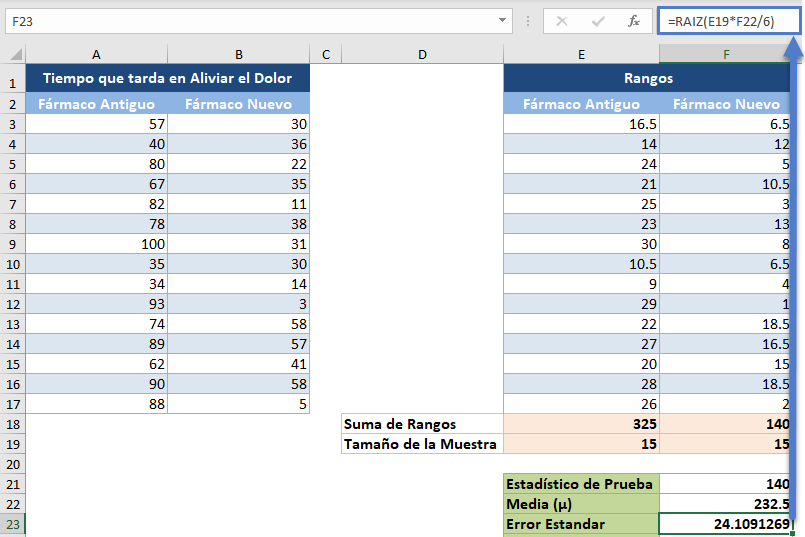
A continuación, calcula la puntuación z de las observaciones mediante la fórmula:
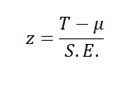
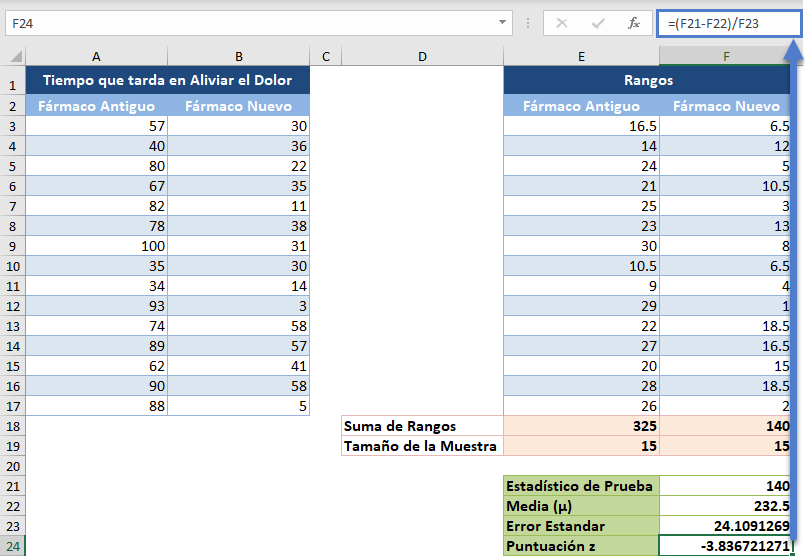
Por último, calcule el valor p de las observaciones utilizando la función DISTR.NORM.N o la función DISTR.NORM.ESTAND.N. Como estamos realizando una prueba de dos colas, multiplicamos el resultado de las funciones DISTR.NORM.N o DISTR.NORM.ESTAND.N por 2.
La función DISTR.NORM.N tiene la sintaxis siguiente DISTR.NORM.N(x, media, desviación estándar, acumulativa), donde es la estadística de la prueba, la media es la calculada a partir de los datos, la desviación estándar es el error estándar, y seleccionamos ‘VERDADERO’ para la función de distribución acumulada.
La función DISTR.NORM.ESTAND.N tiene la sintaxis DISTR.NORM.ESTAND.N(z, acumulada), donde es la puntuación z, y seleccione ‘VERDADERO’ para la función de distribución acumulada.
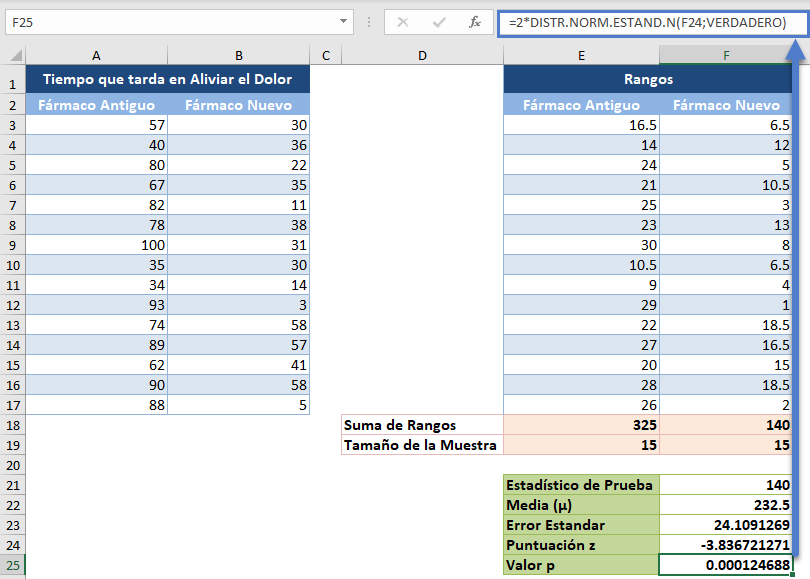
El valor p aquí es el que es menor que nuestro nivel significativo del 5% o 0,05. Por lo tanto, «rechazamos la hipótesis nula», lo que significa que concluimos que hay pruebas estadísticamente significativas de que el nuevo fármaco alivia el dolor de cabeza más rápidamente que el antiguo.
La Prueba de Rango con Signo de Wilcoxon en Google Sheets
La prueba de rangos con signo de Wilcoxon puede calcularse de forma similar en Google Sheets que en Excel, como se muestra a continuación. Para el método del valor crítico, tenemos:
