Prueba de Rango con Signo de Wilcoxon – Excel y Google Sheets
Este tutorial mostrará cómo realizar la Prueba de Rango con Signo de Wilcoxon en Excel y Google Sheets.
Similitudes/diferencias entre la prueba T de Student y la Prueba de Rango con Signo de Wilcoxon
- Tanto la prueba T de Student como la Prueba de Rango con Signo de Wilcoxon se utilizan para determinar si existe una diferencia estadísticamente significativa entre DOS conjuntos de datos, ya sea una muestra contra un valor hipotético, muestras dependientes o muestras emparejadas.
- La prueba T de Student supone que el conjunto de datos procede de una población con distribución normal, pero la prueba de rango con signo de Wilcoxon no hace esta suposición.
Cuándo utilizar la Prueba de Rango con Signo de Wilcoxon
La Prueba de Rango con Signo de Wilcoxon se utiliza cuando alguno de los conjuntos de datos viola la condición de normalidad.
Supuestos para la Prueba de Rango con Signo de Wilcoxon
- Los datos que se miden deben estar en el nivel ordinal o continuo. (Es decir, los datos deben ser una escala clasificada o un número)
- Los datos de la variable independiente deben proceder de un grupo relacionado o de pares emparejados.
- Las diferencias entre los dos grupos relacionados deben ser simétricas.
Cómo realizar la Prueba de Rango con Signo de Wilcoxon en Excel
Tabla de Valores Críticos de la Prueba de Rango con Signo de Wilcoxon
En este método, comparamos las estadísticas de la Prueba de Rango con Signo de Wilcoxon con el valor crítico. A continuación se muestra la guía paso a paso sobre cómo realizar la prueba de rango con signo de Wilcoxon utilizando el método de los valores críticos.
Ejemplo
Antecedentes: Un investigador quiere averiguar si el modo de presentación de un examen tiene algún efecto sobre las puntuaciones de los estudiantes. Seleccionó una muestra aleatoria de 8 estudiantes y les administró una prueba similar utilizando el modo impreso y el modo computarizado. A continuación se muestran las puntuaciones de cada uno de los alumnos en las dos modalidades del test. Pruebe a un nivel de significación del 5% si existe una diferencia significativa en las puntuaciones de los alumnos para los distintos modos de administración de la prueba. El investigador no está seguro de que las distribuciones de las puntuaciones de las pruebas para ambos modos de entrega de la prueba estén distribuidas normalmente.
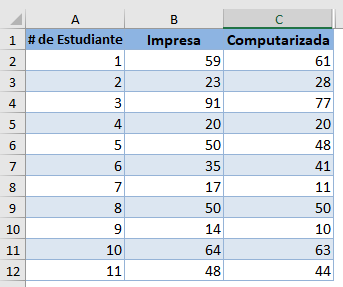
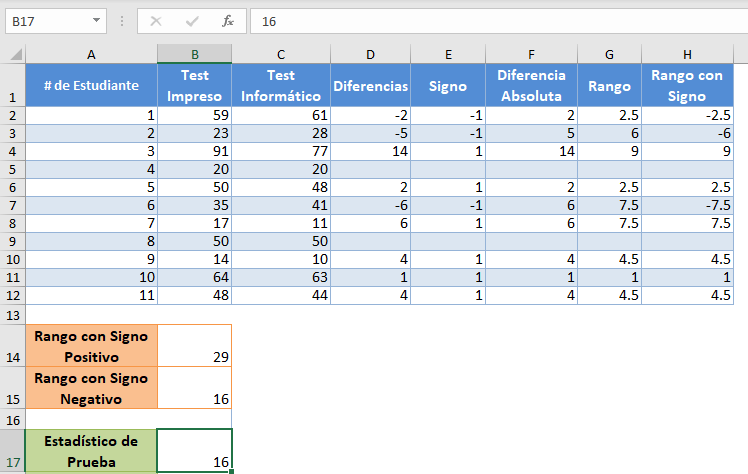
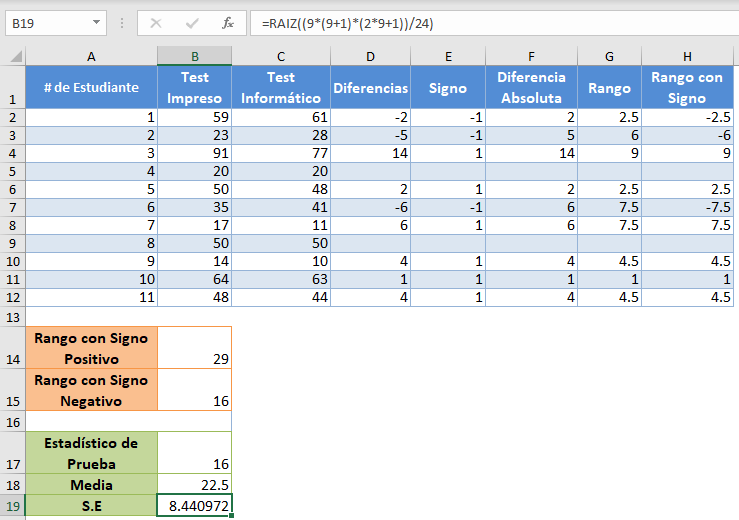
En primer lugar, calcule la diferencia en las puntuaciones de las pruebas de cada uno de los estudiantes restando las puntuaciones «Computarizadas» de las puntuaciones «impresas»:
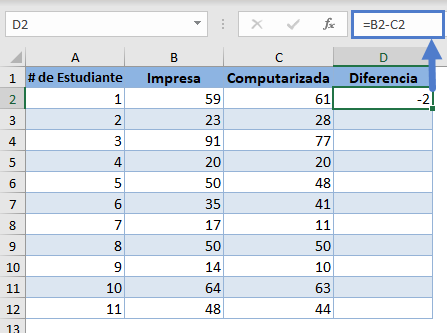
Completa lo mismo para el resto de los estudiantes.
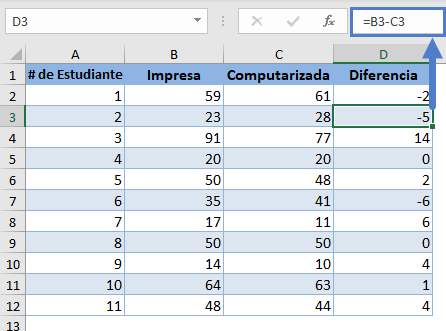
A continuación, elimina las diferencias «0» porque no serán necesarias en los cálculos posteriores, y luego obtén los signos de las diferencias utilizando la función SIGNO. La función SIGNO devuelve -1 para números negativos y 1 para números positivos.
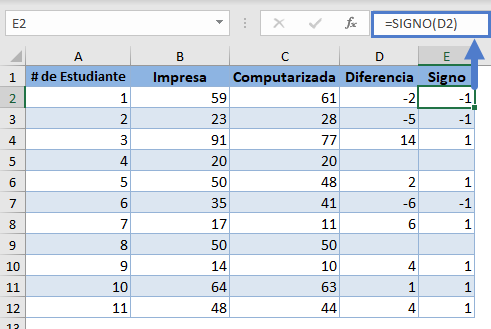
A continuación, obtenga los valores absolutos de las diferencias utilizando la función ABS.
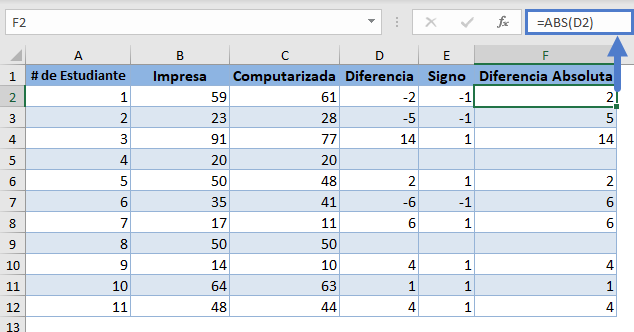
A continuación, obtenga los rangos (en orden ascendente) de las diferencias absolutas utilizando la Función JERARQUIA.MEDIA.
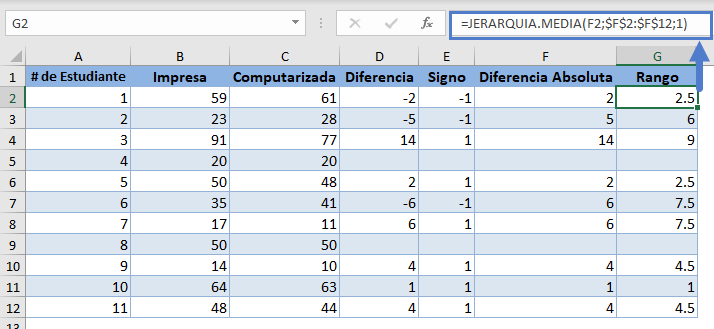
A continuación, multiplique cada rango por el signo correspondiente en la columna Signo para obtener los rangos con signo:
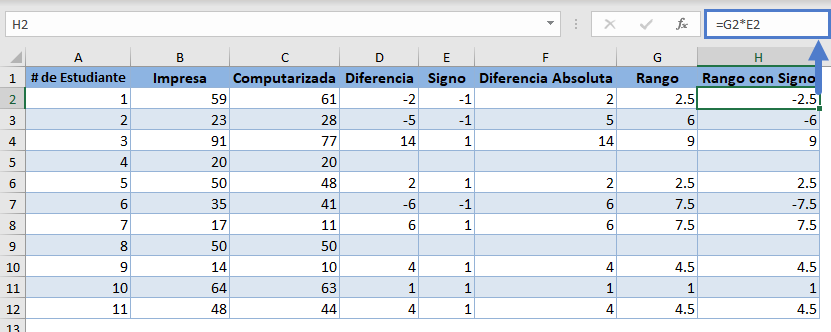
Ahora, vamos a utilizar la función SUMAR.SI para obtener la suma de los Rangos con Signo positivos:
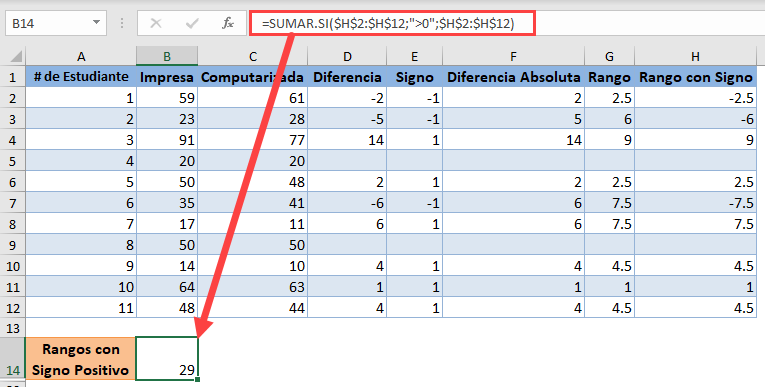
Utilice la función ABS y la función SUMIF para obtener el valor positivo de la suma de los Signed-Ranks negativos:
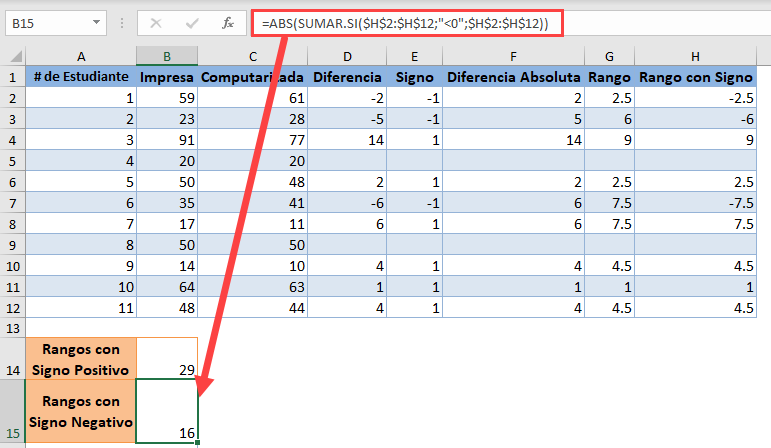
Observe que para la suma de Rangos con Signo positivos, el criterio en la Función CONTAR.SI es «>0» mientras que el criterio para la suma de Rangos con Signo negativos es «<0».
Para la prueba de rango con signo de Wilcoxon, la estadística de la prueba es la menor de la suma del rango con signo positivo y la suma del rango con signo negativo. En nuestro caso, el menor es 16, por lo que nuestro estadístico de prueba es 16.
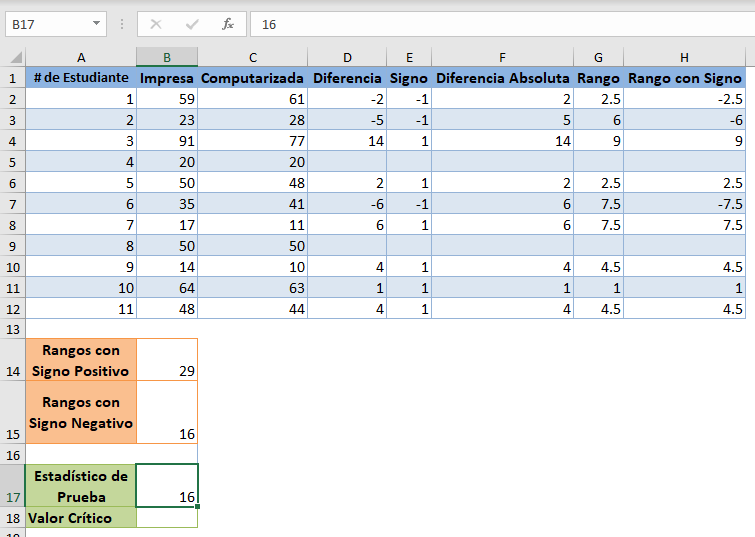
Ahora, obtenga el valor crítico para el tamaño de la muestra de n= 11 y el nivel de significación del 5% de la tabla de valores críticos de Wilcoxon Signed-Rank.
Tenga en cuenta que estamos haciendo una prueba de dos colas aquí porque estamos probando la diferencia en los valores (y no el aumento o la disminución de los valores) que es en ambos sentidos tanto el aumento como la disminución de los valores.
A continuación se muestra un extracto de la tabla Wilcoxon Signed-Rank de valores críticos:
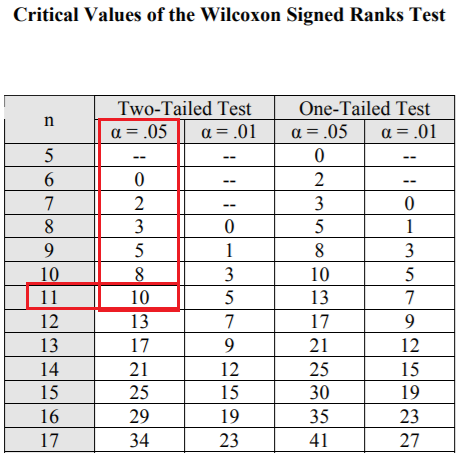Por lo tanto, el valor crítico es 10.
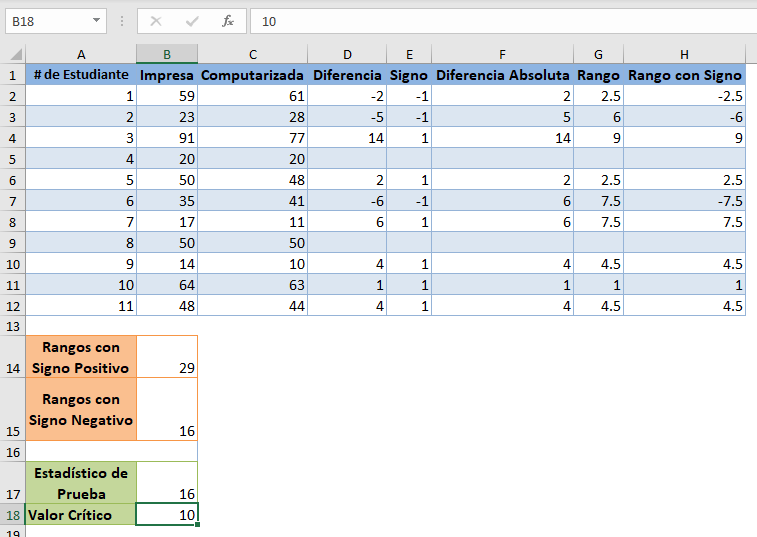
Para la Prueba de Rango con Signo de Wilcoxon, concluimos que existe una diferencia significativa entre las variables cuando la Estadística de Prueba es menor que el valor crítico.
En este caso, el estadístico de la prueba es 16 y el valor crítico es 10, puesto que el estadístico de la prueba es mayor que el valor crítico, concluimos que no hay pruebas estadísticamente significativas de que el modo de administración de una prueba afecte a las puntuaciones de los alumnos.
Método del Valor p
Otro método para realizar la prueba de Wilcoxon Signed-Rank es aproximar la distribución a una distribución normal y luego utilizar el valor p de la puntuación z aproximada o la puntuación t, dependiendo del tamaño de la muestra.
En los siguientes pasos, ilustramos este método usando el mismo ejemplo utilizado en el método anterior.
Antecedentes: Un investigador quiere averiguar si el modo de realización de un examen tiene algún efecto sobre las puntuaciones de los alumnos en el mismo. Seleccionó una muestra aleatoria de 8 alumnos y les administró un test similar en modo impreso y en modo informático. A continuación se muestran las puntuaciones de cada uno de los alumnos en las dos modalidades del test. Pruebe a un nivel de significación del 5% si existe una diferencia significativa en las puntuaciones de los alumnos para los distintos modos de administración de la prueba. El investigador no está seguro de que las distribuciones de las puntuaciones de las pruebas para ambos modos de entrega de la prueba estén distribuidas normalmente.
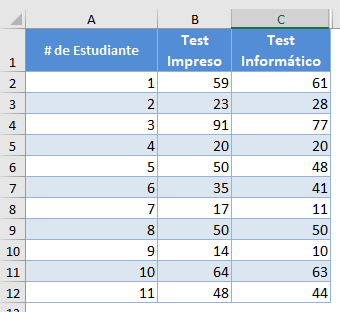
Vamos a seguir todos los pasos descritos en el método anterior para obtener nuestro estadístico de prueba (T). Recuerde que el estadístico de prueba es el menor de la suma de los rangos con signo positivo y el valor absoluto de la suma de los rangos con signo negativo.
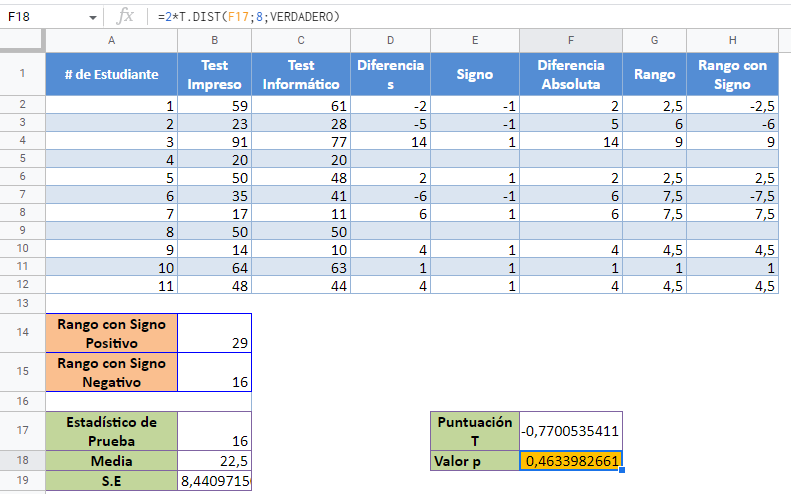
Ahora, obtendremos la media y el error estándar de la distribución. La media ( μ) de la distribución viene dada por: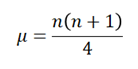 
donde n es el tamaño de la muestra, y el error estándar viene dado por: 
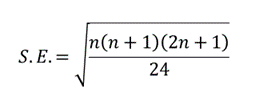Para nuestro caso, n=9 después de eliminar las diferencias «0». Entonces, calculamos la media de la siguiente manera:
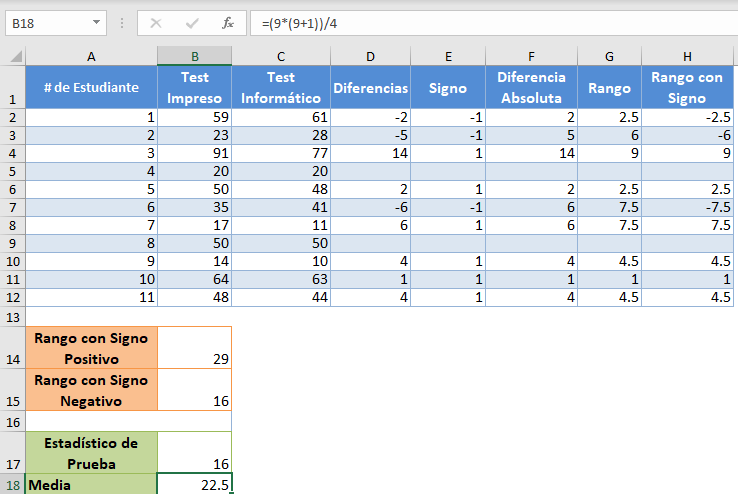
y el error estándar como sigue:
A continuación, calcule la puntuación t de las observaciones mediante la fórmula: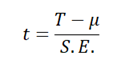 
Por último, calcule el valor p de las observaciones utilizando la función DISTR.T.N. Para la función DISTR.T.N, x es la puntuación t, el grado de libertad es n-1=9-1=8, y seleccione ‘VERDADERO’ para la función de distribución acumulativa. Además, como estamos realizando una prueba de dos colas, multiplicamos el resultado de la función DISTR.T.N por 2.
El valor p aquí es 0,463, que es mayor que nuestro nivel de significación del 5% o 0,05. Por lo tanto, «no se rechaza la hipótesis nula», lo que significa que concluimos que no hay pruebas estadísticamente significativas de que el modo de administración de un examen afecte a las puntuaciones de los alumnos.
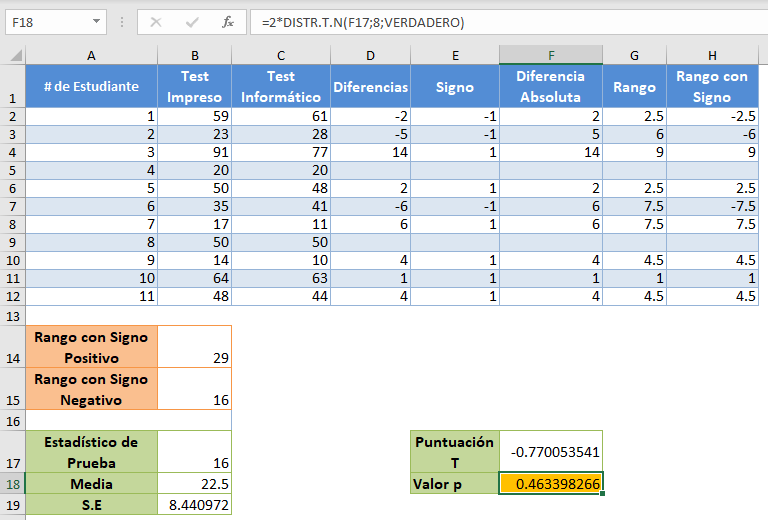
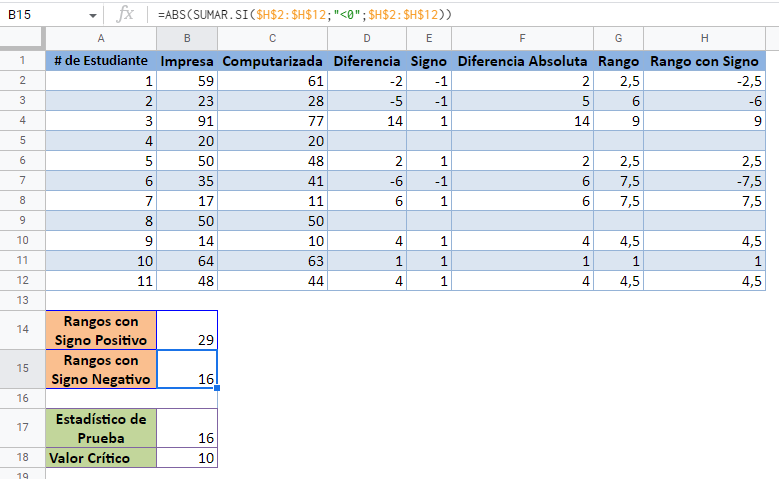
Prueba de Rango con Signo de Wilcoxon en Google Sheets
La Prueba de Rango con Signo de Wilcoxon puede calcularse de forma similar en Google Sheets que en Excel, como se muestra a continuación. Para el método del valor crítico, tenemos:
y cuando se utiliza el valor p tenemos:
