Intervalos de Confianza en Excel y Google Sheets

Este tutorial demostrará cómo crear intervalos de confianza en Excel y Google Sheets.

Los intervalos de confianza (IC) proporcionan el rango de valores en el que debería situarse la media real (el promedio) de una población. Suele mostrarse como:

Los intervalos de confianza se calculan a partir de una media muestral de la población, utilizando un «nivel de confianza». Por ejemplo, un nivel de confianza del 99% da más seguridad de que la media real estará dentro del intervalo de confianza que un nivel de confianza del 90%.

Cómo Calcular los Intervalos de Confianza en Excel

Hay tres maneras de calcular los intervalos de confianza en Excel:

1. Las funciones INTERVALO.CONFIANZA.NORM o INTERVALO.CONFIANZA.T.
2. La opción de Estadísticas Descriptivas del botón de Análisis de Datos en la sección de Datos
3. Calcular manualmente el Intervalo de Confianza.

Funciones de CONFIANZA

Las funciones INTERVALO.CONFIANZA.NORM y INTERVALO.CONFIANZA.T devuelven el margen de error utilizado para calcular el intervalo de confianza.

Cuándo Utilizar INTERVALO.CONFIANZA.NORM vs. INTERVALO.CONFIANZA.T

• La función .NORM se utiliza cuando se conoce la desviación estándar de la población.
• La función .T se utiliza cuando la desviación estándar de la población es desconocida.

Sin embargo, según el Teorema Central del Límite (CLT), un poderoso teorema estadístico, si la muestra es suficientemente grande (normalmente 30 o más), la desviación estándar de la muestra puede utilizarse para aproximar la desviación estándar de la población.

En otras palabras, utilice la función INTERVALO.CONFIANZA.NORM cuando la desviación estándar de la población es conocida, o cuando la desviación estándar de la población es desconocida, pero el tamaño de la muestra es de 30 o más.

Sintaxis de las Funciones de Confianza

=INTERVALO.CONFIANZA.NORM(Alfa, desviación estándar, tamaño de la muestra)

=INTERVALO.CONFIANZA.T(Alfa, desviación típica, tamaño de la muestra)

Alfa es el nivel de significación que se obtiene restando el nivel de confianza a 1. Por ejemplo, supongamos que se quiere calcular el intervalo de confianza del 95% de la media, el nivel de significación (alfa) corresponde a 1-0,95 = 0,05 . Los niveles de confianza más populares que suelen utilizarse para calcular los intervalos de confianza son el 90%, el 95% y el 99%.

Ejemplo de INTERVALO.CONFIANZA.NORM

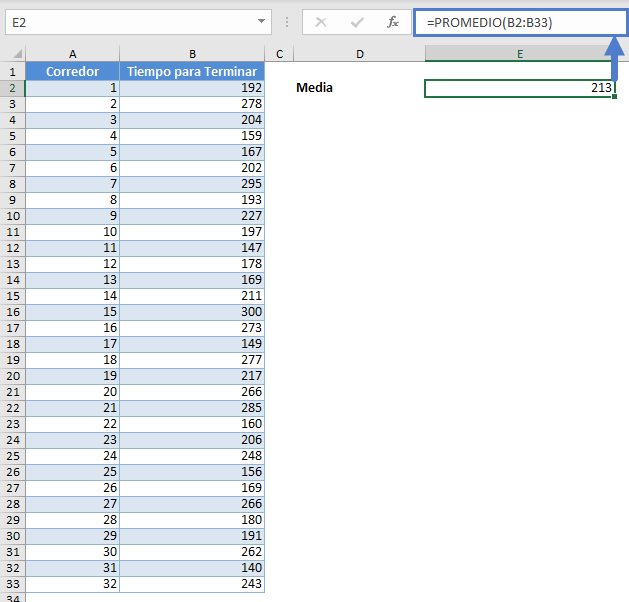
Antecedentes: Se supone que el tiempo, en minutos, para terminar un maratón se distribuye normalmente. Se ha realizado un seguimiento de una muestra aleatoria de corredores de maratón y a continuación se presenta el tiempo que tardan en terminar un maratón. Calculemos un intervalo de confianza del 95% para la media (promedio) del tiempo que tardan todos los corredores en correr un maratón. En primer lugar, calculemos la media muestral (promedio) de la muestra utilizando la función PROMEDIO.

A continuación, calcule la desviación estándar (SD) de la muestra utilizando la función DESVEST.M.

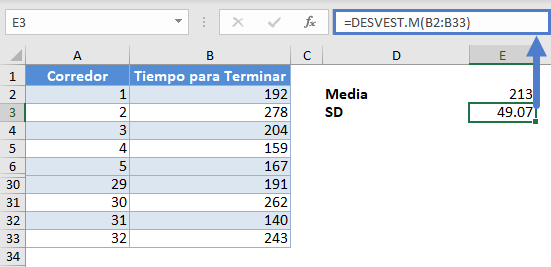
Nota: La función DESVEST.M se utiliza para calcular la desviación estándar de la muestra, mientras que DESVEST.P se utiliza para calcular la desviación estándar de la población. Al calcular los intervalos de confianza, utilice siempre la función DESVEST.M para calcular la desviación estándar de la muestra.

A continuación, calcule el tamaño de la muestra utilizando la función CONTAR.

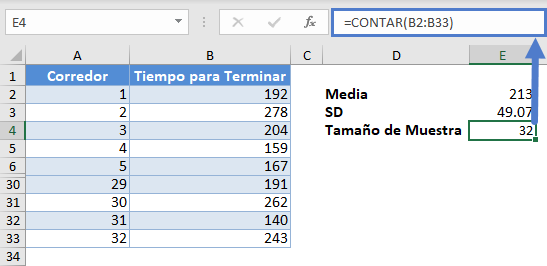
Para calcular un intervalo de confianza del 95%, el alfa (nivel significativo) es 1-0,95 = 0,05. Ahora, calcule el margen de error utilizando la función INTERVALO.CONFIANZA.NORM.

Nota: estamos utilizando la Función INTERVALO.CONFIANZA.NORM aquí porque, de acuerdo con el Teorema del Límite Central (CLT), podemos aproximar la desviación estándar de la población utilizando la desviación estándar de la muestra si el tamaño de la muestra es 30 o más.

Utilice la Función CONCATENAR para mostrar el intervalo de confianza sumando y restando el margen de error de la media.

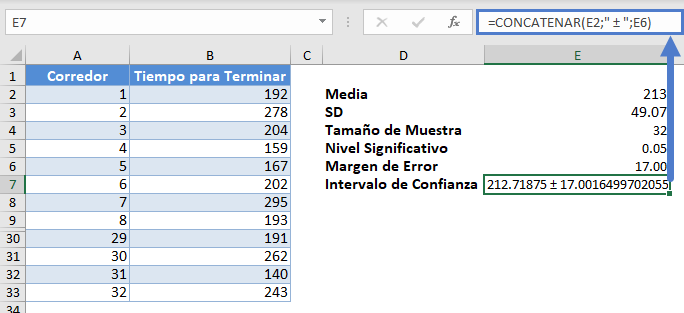
Nota: La función CONCATENAR no redondea los valores. Así que vamos a añadir la Función REDONDEAR a la fórmula para que nuestro resultado sea más fácil de leer.

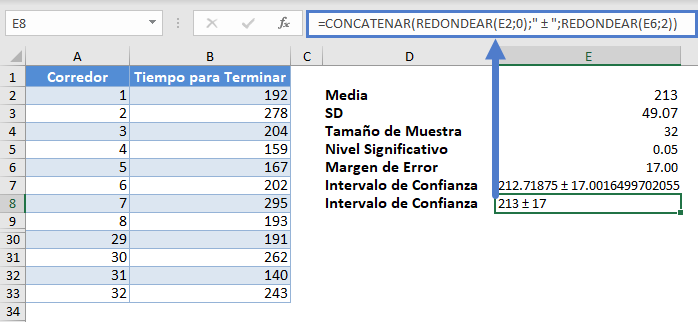
Nuestro Intervalo de Confianza para la media de la población es 213±17 o simplemente (196,230) .

Ejemplo de INTERVALO.CONFIANZA.T

Antecedentes: Se supone que el Cociente de Inteligencia de los estudiantes universitarios de Estados Unidos sigue una distribución normal. Los cocientes inteligentes de una muestra aleatoria de 5 estudiantes universitarios estadounidenses son los que se muestran a continuación. Calculemos un intervalo de confianza del 99% para la media (promedio) del cociente inteligente de todos los estudiantes universitarios de Estados Unidos.

En este caso, el alfa (nivel de significación) es 1-0,99 = 0,01.

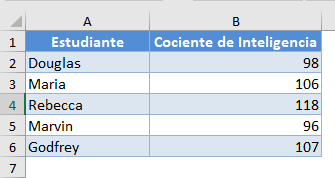
Siga los pasos del ejemplo anterior para calcular la media, la desviación estándar (SD) y el tamaño de la muestra.

Ahora, calcule el Margen de Error utilizando la función INTERVALO.CONFIANZA.T en Excel.

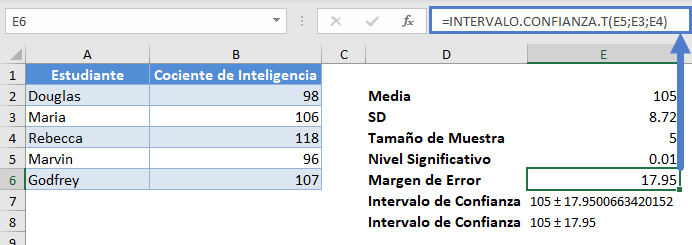
Nota: utilizamos la función INTERVALO.CONFIANZA.T aquí porque no conocemos la desviación estándar de la población, y el tamaño de la muestra es pequeño (menos de 30).

El intervalo de confianza para la media de la población es 105±17,95 o simplemente (87,05 , 122,95).

Calcular los Intervalos de Confianza utilizando estadísticas descriptivas

Otro método alternativo para calcular los Intervalos de Confianza en Excel es utilizando la función de Estadísticas Descriptivas. Esta función se encuentra en la cinta de datos > Análisis de datos.

Si no ve la opción de Análisis de datos, deberá instalar el paquete de herramientas de análisis de datos.

En la ventana de Análisis de Datos, seleccione Estadísticas Descriptivas y haga clic en Aceptar.

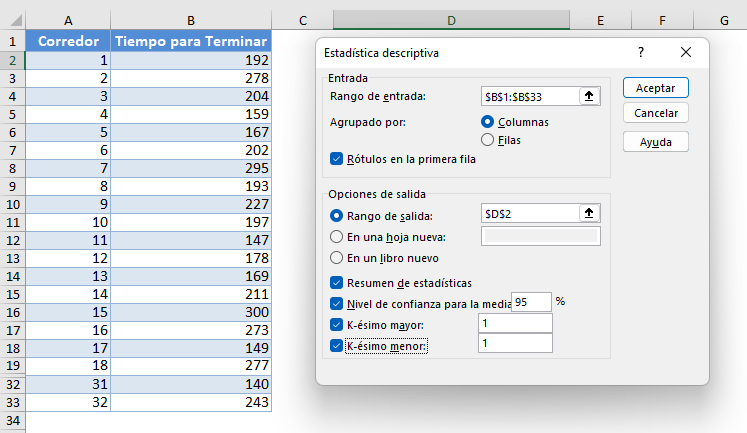
A continuación, deberá configurar los parámetros.

• Haga clic en «Rango de entrada» y seleccione las celdas que contienen los datos de origen.
• En la sección «Agrupado por», seleccione la casilla de radio «Columnas».
• Seleccione la casilla «Etiquetas en la primera fila» si el rango seleccionado contiene cabeceras de columna como se muestra en el ejemplo siguiente.
• Seleccione la opción de salida deseada. Para obtener los resultados en la misma hoja, seleccione el rango de salida y especifique la referencia específica de la celda en la que se mostrará la matriz. En nuestro caso es $D$2
• Marque la casilla «Nivel de confianza para la media» e introduzca el nivel de confianza deseado, en nuestro caso el 95% para el ejemplo 1 y el 99% para el ejemplo 2.
• También puede marcar las otras casillas de verificación, para obtener más valores estadísticos descriptivos para los datos, incluyendo las casillas de verificación «Resumen de estadísticas», «K-ésimo Mayor» y «K-ésimo menor».

La salida para el primer ejemplo es la siguiente:

Del resultado anterior, el valor de confianza (margen de error) es de aproximadamente 17,69. Para obtener el intervalo de confianza, sumamos y restamos el valor de confianza de la media como se muestra: 213±17,69 para obtener (195,31, 230,69) como intervalo de confianza.

Fórmula del Intervalo de Confianza en Excel

También puede calcular los intervalos de confianza utilizando directamente la fórmula del intervalo de confianza. La fórmula para el intervalo de confianza del 100(1-α)% viene dada por:

Media ± z_crit (o t_crit) * (Desviación estándar / Raíz cuadrada del tamaño de la muestra)

z_crit (o t_crit) * (Desviación estándar /Raíz cuadrada del tamaño de la muestra) es el margen de error.

• Utilice z_crit cuando se conozca la desviación estándar de la población.
• Utilice t_crit cuando la desviación estándar de la población sea desconocida.
• Utilice z_crit cuando la desviación estándar de la población es desconocida pero la muestra es de 30 o más.

Excel no tiene una función especial para obtener el z_crit de cualquier nivel de confianza. Sin embargo, para el t_crit, la función INV.T.2C da el t_crit para cualquier nivel de confianza y grado de libertad dados. Hablaremos más sobre esta función en el ejemplo 2. Para los niveles de confianza populares, 90%, 95% y 99%, el zcrit es 1,645, 1,96 y 2,576 respectivamente.

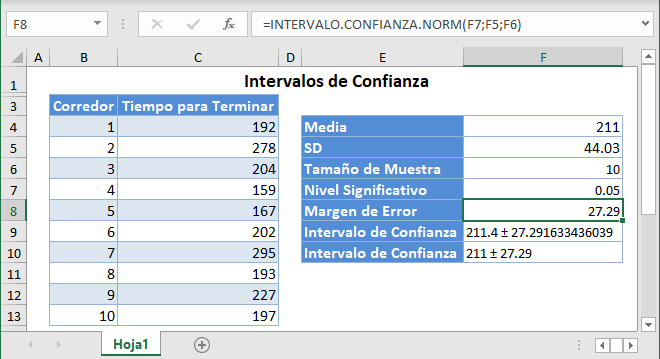
Para el ejemplo 1, utilizaremos 1,96 como z_crit para nuestro intervalo de confianza del 95%. El procedimiento se muestra a continuación:

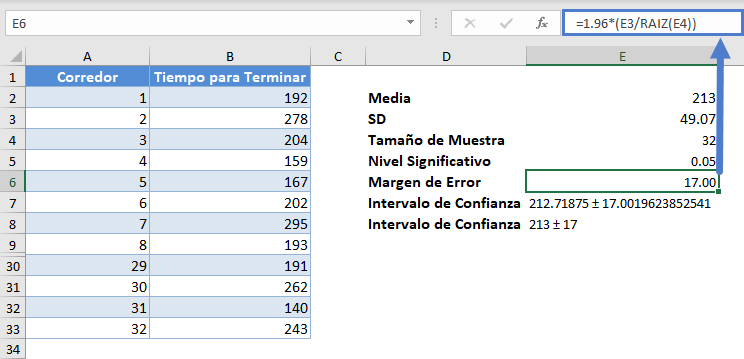
El margen de error da 17,00 y, como es habitual, el intervalo de confianza es Media ± Margen de error que es 213±17 o (213-17,213+17)=(196,230).

Para el ejemplo 2, como la desviación estándar de la población es desconocida y la muestra es pequeña, utilizaremos la función INV.T.2C para obtener el t_crit del intervalo de confianza del 99%. La función INV.T.2C toma dos argumentos: la probabilidad (alfa) y el grado de libertad. Al encontrar intervalos de confianza, alfa sirve como probabilidad. El grado de libertad (df) se obtiene restando 1 al tamaño de la muestra. Así, para nuestro caso, df = 5 – 1 = 4.

Así, seguimos los siguientes pasos para calcular directamente los intervalos de confianza cuando la desviación típica de la población es desconocida y la muestra es pequeña.

Primero, utilice los métodos ilustrados en los ejemplos anteriores para calcular la media, la desviación estándar, el tamaño de la muestra y el nivel de significación. A continuación, obtenga el grado de libertad.

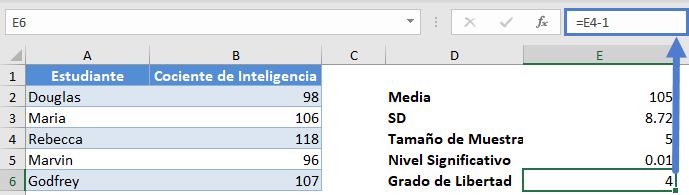
A continuación, obtenga el valor crítico (t_crit).

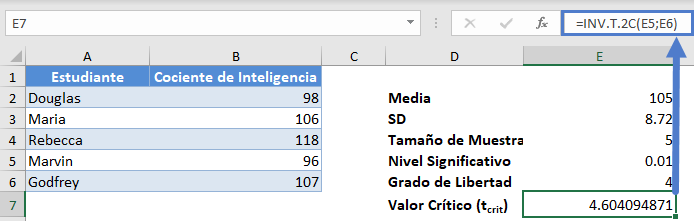
Ahora, calcula el margen de error.

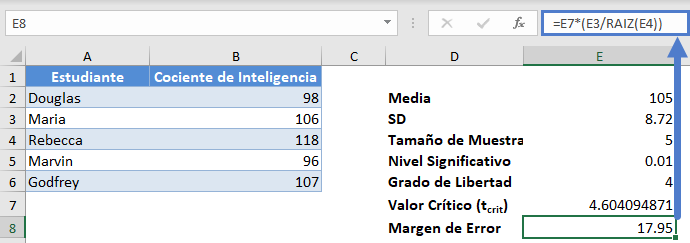
Por último, presente el intervalo de confianza.

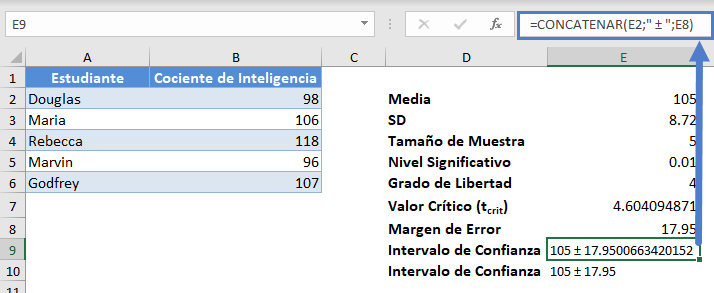
El margen de error da 17,95, y como es habitual, el intervalo de confianza es Media ± Margen de error que es 105±17,95 o (105-17,95,105+17,95)=(87,05,122,95).

Intervalos de Confianza en Google Sheets

Los Intervalos de Confianza pueden ser calculados usando métodos similares en Google Sheets. Puedes utilizar las funciones CONFIDENCE.NORM y CONFIDENCE.T.

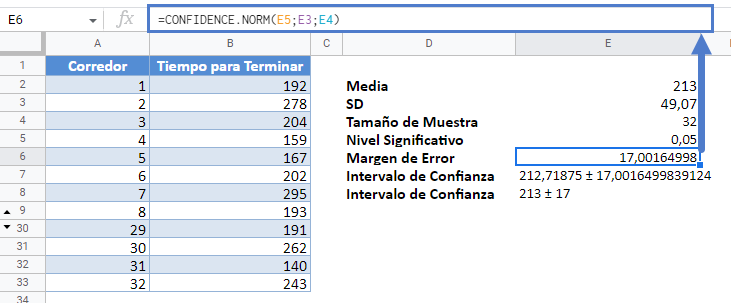
O calcular el intervalo de confianza manualmente:

Intervalo de Confianza – XLMiner Analysis Toolpak

Google Sheets no tiene el paquete de herramientas de análisis de datos, en su lugar tiene el complemento XLMiner Analytis Toolpak.

Una vez que haya instalado este complemento, puede encontrarlo en la pestaña Complementos . Seleccione XLMiner Analysis ToolPak y haga clic en Iniciar.

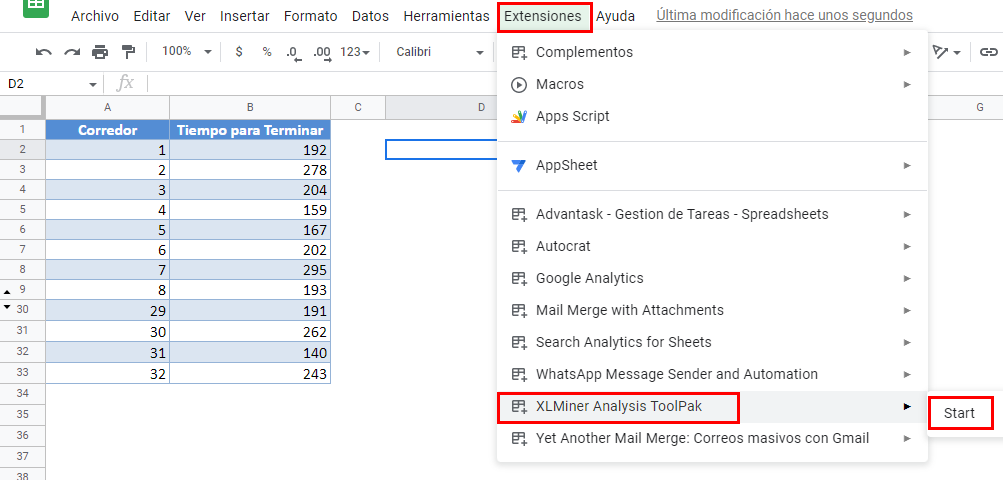
En la ventana de XLMiner Analysis ToolPak, seleccione Descriptive Statistics.

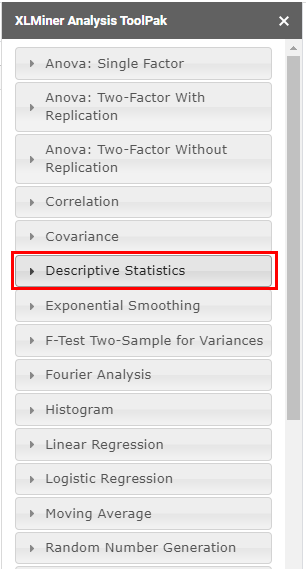
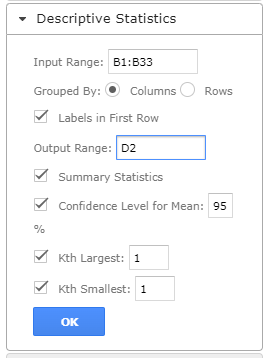
En el menú desplegable de la opción Estadísticas Descriptivas, configure los parámetros de la siguiente manera.

• Seleccione las celdas que contienen los datos de origen y haga clic en la casilla «Rango de entrada».
• En la sección «Agrupado por», seleccione la casilla «Columnas».
• Seleccione la casilla «Etiquetas en la primera fila» si el rango seleccionado contiene cabeceras de columna, como se muestra en el ejemplo siguiente.
• Introduzca la celda o el rango de salida deseado en la casilla «Rango de salida».
• Marque la casilla «Nivel de confianza para la media» e introduzca el nivel de confianza deseado, en nuestro caso el 95%.
• También puede marcar las otras casillas de verificación, para obtener más valores estadísticos descriptivos para los datos, incluyendo las casillas de verificación «Estadísticas de resumen», «Kth Mayor» y «Kth Menor».
• A continuación, haga clic en «Aceptar».

El resultado es el siguiente:

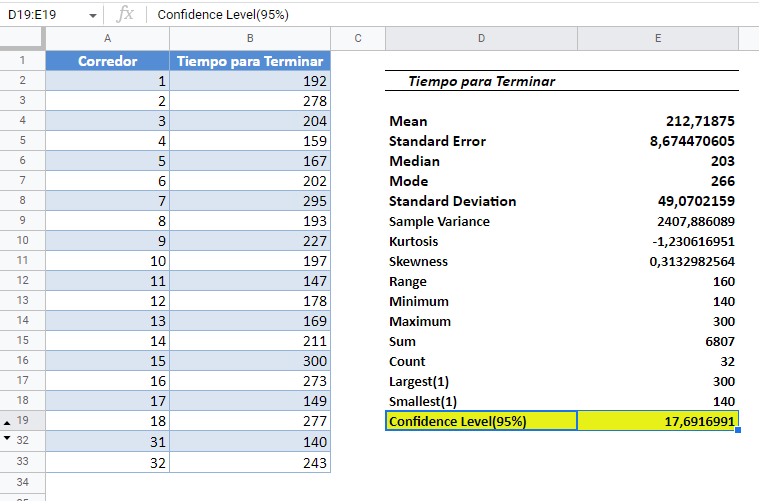
A partir del resultado anterior, el valor de confianza (margen de error) es aproximadamente 17,69.

Para obtener el intervalo de confianza, sumamos y restamos el valor de confianza de la media como se muestra: 213±17,69 para obtener (195,31,230,69) como intervalo de confianza.