Wilcoxon-Vorzeichen-Rang-Test – Excel und Google Sheets
In diesem Tutorial zeigen wir Ihnen, wie Sie den Wilcoxon-Vorzeichen-Rang-Test in Excel und Google Sheets durchführen können.
Der Wilcoxon-Vorzeichen-Rang-Test ist ein nicht parametrischer Test, der eine Reihe von angepassten Stichproben verwendet, um die Standorte zweier Grundgesamtheiten zu vergleichen. Er erfüllt eine ähnliche Funktion wie der Student-t-Test für gepaarte Stichproben mit der Ausnahme, dass er im Gegensatz zum T-Test für gepaarte Stichproben keine Normalität der Grundgesamtheit voraussetzt.
Der Wilcoxon-Vorzeichen-Rang-Test kann auch verwendet werden, um die Lage einer Reihe von Stichproben mit einem hypothetischen Median zu vergleichen. Er erfüllt dieselbe Funktion wie der Student-T-Test für eine Stichprobe.
Gemeinsamkeiten/Unterschiede zwischen dem Student-T-Test und dem Wilcoxon-Vorzeichen-Rang-Test
- Sowohl der Student-T-Test als auch der Wilcoxon-Vorzeichen-Rang-Test werden verwendet, um festzustellen, ob ein statistisch signifikanter Unterschied zwischen ZWEI Datensätzen besteht (entweder zwischen einer Stichprobe und dem hypothetischen Wert, abhängigen Stichproben oder übereinstimmenden/gepaarten Stichproben).
- Beim Student-T-Test wird davon ausgegangen, dass der Datensatz aus einer normalverteilten Grundgesamtheit stammt, aber beim Wilcoxon Signed-Rank-Test wird diese Annahme nicht gemacht.
Wann wird der Wilcoxon-Vorzeichen-Rang-Test verwendet?
Der Wilcoxon-Vorzeichen-Rang-Test wird verwendet, wenn einer der Datensätze gegen die Normalitätsbedingung verstößt.
Annahmen für den Wilcoxon-Vorzeichen-Rang-Test
- Die zu messenden Daten müssen sich auf der ordinalen oder kontinuierlichen Ebene befinden. (d. h. die Daten müssen eine Rangskala oder eine Zahl sein.)
- Die Daten der unabhängigen Variablen sollten von einer verwandten Gruppe oder von übereinstimmenden Paaren stammen.
- Die Unterschiede zwischen den beiden verwandten Gruppen müssen symmetrisch sein.
Den Wilcoxon-Vorzeichen-Rang-Test in Excel durchführen
Wilcoxon-Vorzeichen-Rang-Test – Tabelle der kritischen Werte
Bei dieser Methode wird die Statistik des Wilcoxon-Vorzeichen-Rang-Tests mit dem kritischen Wert verglichen. Im Folgenden finden Sie eine schrittweise Anleitung zur Durchführung des Wilcoxon-Vorzeichen-Rang-Tests mit der Methode der kritischen Werte.
Beispiel
Hintergrund: Ein Forscher möchte herausfinden, ob die Art der Durchführung eines Tests einen Einfluss auf die Testergebnisse der Studenten hat. Er wählte eine Zufallsstichprobe von 8 Studenten aus und ließ sie einen ähnlichen Test in gedruckter und in computergestützter Form ablegen. Die Ergebnisse der Studenten in den beiden Testmodi sind unten dargestellt. Prüfen Sie auf einem Signifikanzniveau von 5 %, ob ein signifikanter Unterschied in den Punktzahlen der Studenten für die verschiedenen Testarten besteht. Der Forscher ist sich nicht sicher, ob die Verteilungen der Testergebnisse für beide Testdurchführungsarten normalverteilt sind.
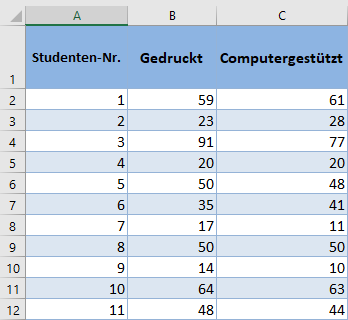
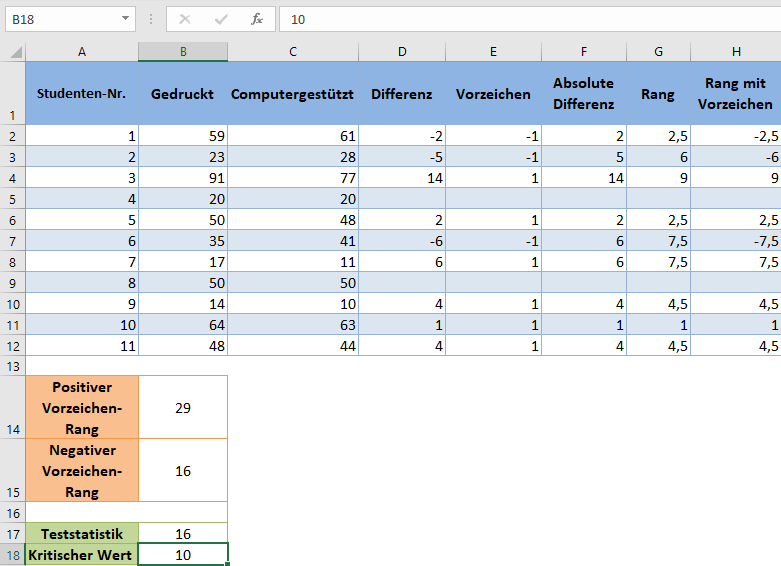
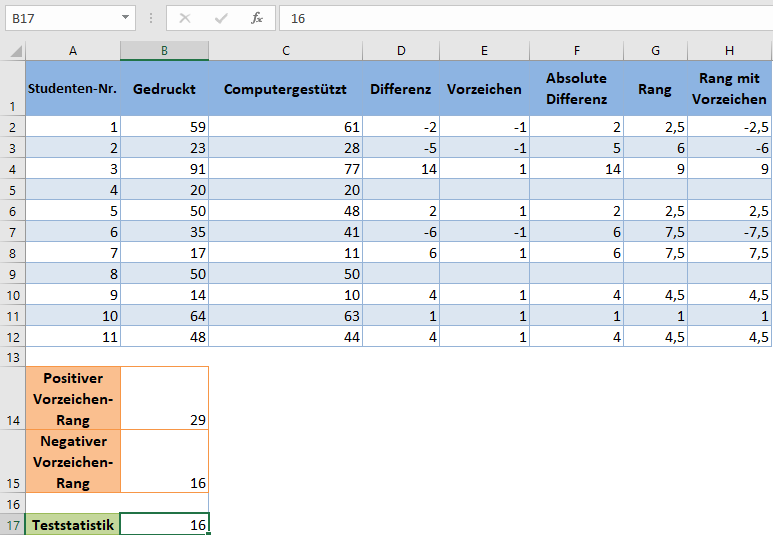
Berechnen Sie zunächst die Differenz zwischen den Testergebnissen der einzelnen Studenten, indem Sie die Ergebnisse für „Computergestützt“ von den Ergebnissen für „Gedruckt“ abziehen:
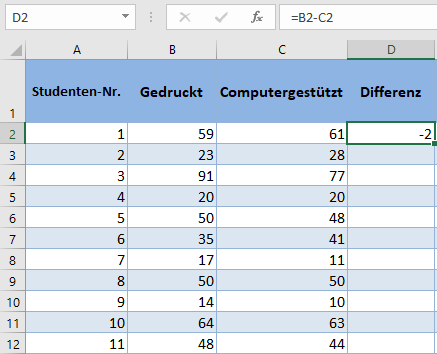
Führen Sie das Gleiche für die übrigen Studenten durch.
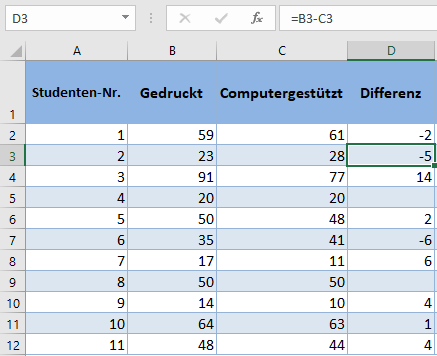
Entfernen Sie als Nächstes die „Null“-Differenzen, da sie für weitere Berechnungen nicht benötigt werden und ermitteln Sie dann die Vorzeichen der Differenzen mithilfe der VORZEICHEN-Funktion. Die VORZEICHEN-Funktion gibt -1 für negative Zahlen und 1 für positive Zahlen zurück.
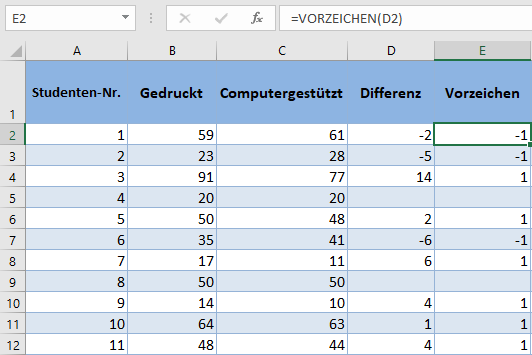
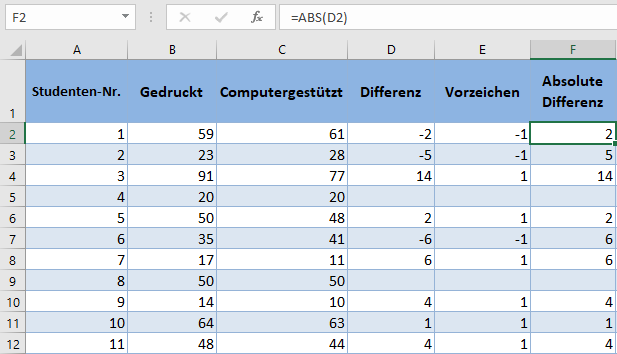
Als Nächstes erhalten Sie die absoluten Werte der Differenzen mit der ABS-Funktion.
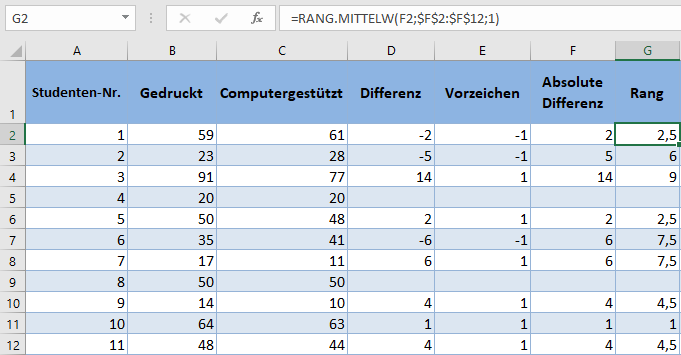
Als nächstes erhalten Sie die Ränge (in aufsteigender Reihenfolge) der absoluten Differenzen mit der RANG.MITTELW-Funktion.
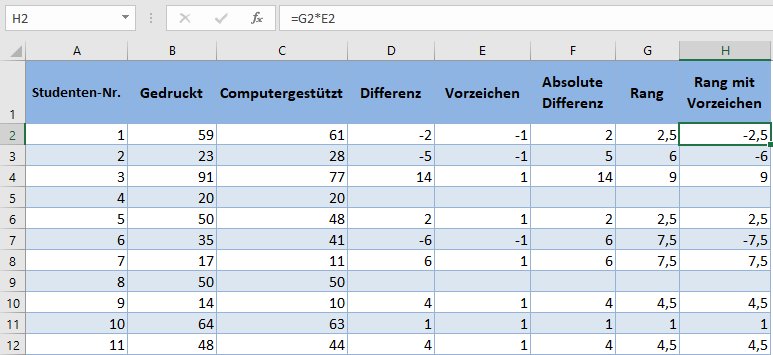
Multiplizieren Sie dann jeden Rang mit dem entsprechenden Vorzeichen in der Spalte Vorzeichen, um die Ränge mit Vorzeichen zu erhalten:
Nun verwenden wir die SUMMEWENN-Funktion, um die Summe der Ränge mit positiven Vorzeichen zu erhalten:
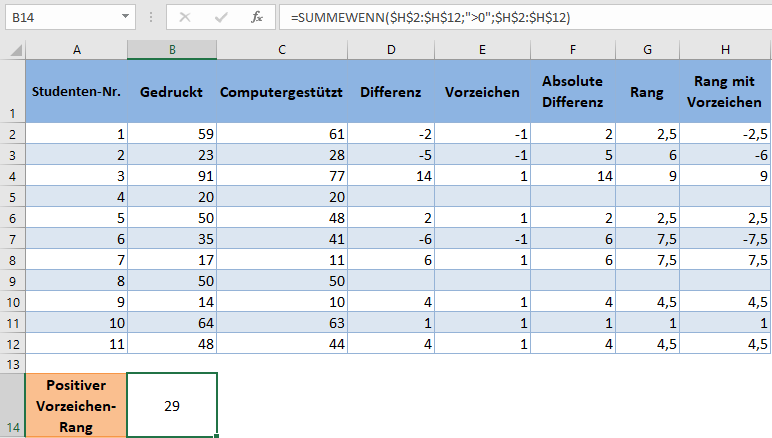
Verwenden Sie die ABS- und SUMMEWENN-Funktion, um den positiven Wert der Summe der Ränge mit negativen Vorzeichen zu erhalten:
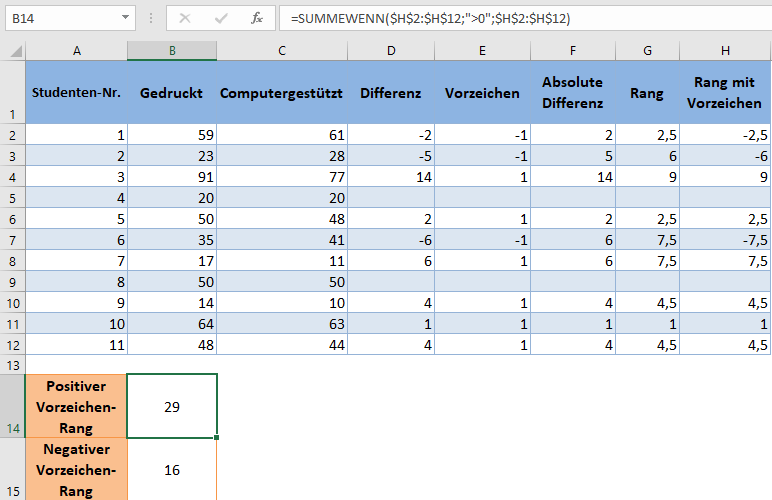
Beachten Sie, dass das Kriterium für die Summe mit positivem Vorzeichen in der SUMMEWENN-Funktion „>0“ ist, während das Kriterium für die Summe mit negativem Vorzeichen „<0“ ist.
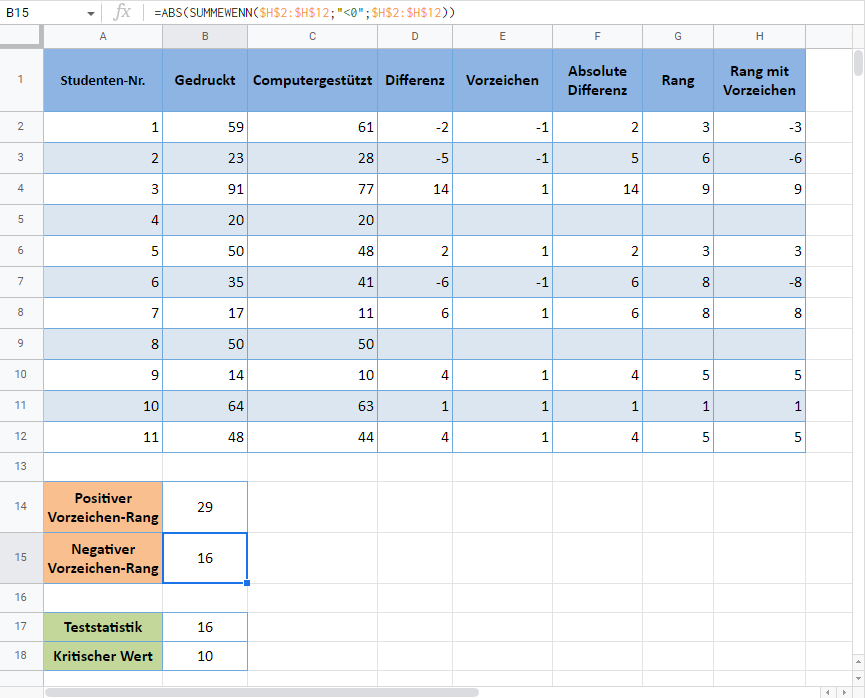
Beim Wilcoxon-Vorzeichen-Rang-Test entspricht die Teststatistik dem kleineren Wert aus der Rangsumme mit positivem Vorzeichen und der Rangsumme mit negativem Vorzeichen. In unserem Fall ist der kleinere Wert 16, also ist unsere Teststatistik 16.
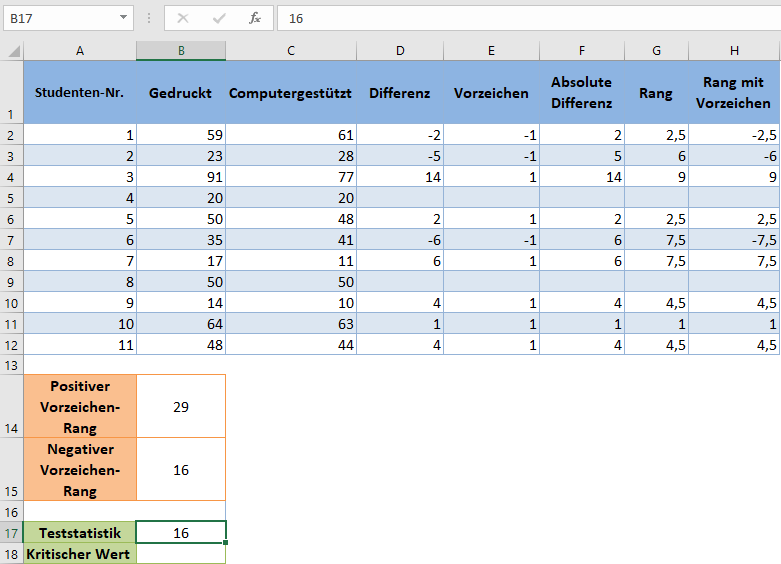
Der kritische Wert für den Stichprobenumfang von n= 11 und das Signifikanzniveau von 5 % wird nun aus der Wilcoxon-Vorzeichen-Rang-Tabelle der kritischen Werte ermittelt.
Beachten Sie, dass wir hier einen zweiseitigen Test durchführen, da wir auf die Differenz der Werte und nicht auf die Zunahme oder Abnahme der Werte testen, was sowohl eine Zunahme als auch eine Abnahme der Werte bedeutet.
Ein Auszug aus der Wilcoxon-Vorzeichen-Rang-Tabelle der kritischen Werte ist unten dargestellt:
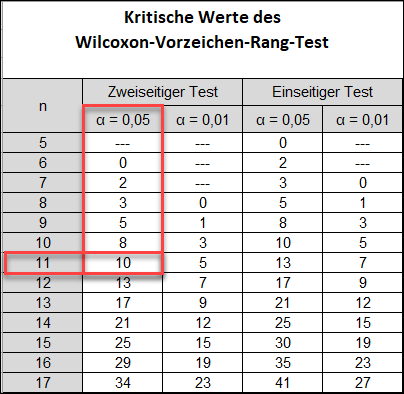
Der kritische Wert ist also 10.
Beim Wilcoxon-Vorzeichen-Rang-Test kommen wir zu dem Schluss, dass ein signifikanter Unterschied zwischen den Variablen besteht, wenn die Teststatistik kleiner als der kritische Wert ist.
In diesem Fall beträgt die Teststatistik 16 und der kritische Wert 10. Da die Teststatistik größer als der kritische Wert ist, schließen wir, dass es keinen statistisch signifikanten Beweis dafür gibt, dass die Art der Durchführung eines Tests die Testergebnisse der Studenten beeinflusst.
Die p-Wert-Methode
Eine andere Methode zur Durchführung des Wilcoxon-Vorzeichen-Rang-Tests besteht darin, die Verteilung an eine Normalverteilung anzunähern und dann den p-Wert des angenäherten z-Werts oder t-Werts je nach Stichprobengröße zu verwenden.
In den folgenden Schritten wird diese Methode anhand des gleichen Beispiels wie bei der vorherigen Methode veranschaulicht.
Hintergrund: Ein Forscher möchte herausfinden, ob die Art der Durchführung eines Tests einen Einfluss auf die Testergebnisse der Studenten hat. Er wählte eine Zufallsstichprobe von 8 Schülern aus und ließ sie einen ähnlichen Test in gedruckter und in computergestützter Form durchführen. Die Ergebnisse der Studenten in den beiden Testmodi sind unten dargestellt. Prüfen Sie auf einem Signifikanzniveau von 5 %, ob ein signifikanter Unterschied in den Punktzahlen der Studenten für die verschiedenen Testarten besteht. Der Forscher ist sich nicht sicher, ob die Verteilungen der Testergebnisse für beide Testdurchführungsarten normalverteilt sind.

Wir werden alle in der vorherigen Methode beschriebenen Schritte durchführen, um unsere Teststatistik (T) zu erhalten. Denken Sie daran, dass die Teststatistik der kleinere Wert aus der Summe der Ränge mit positiven Vorzeichen und dem absoluten Wert der Summe der Ränge mit negativen Vorzeichen ist.
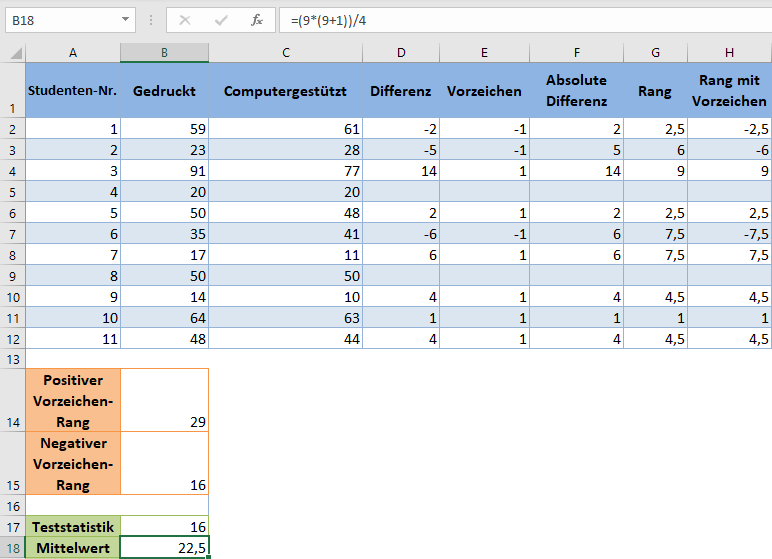
Nun werden wir den Mittelwert und den Standardfehler der Verteilung ermitteln. Der Mittelwert ( μ) der Verteilung ist gegeben durch:
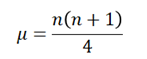
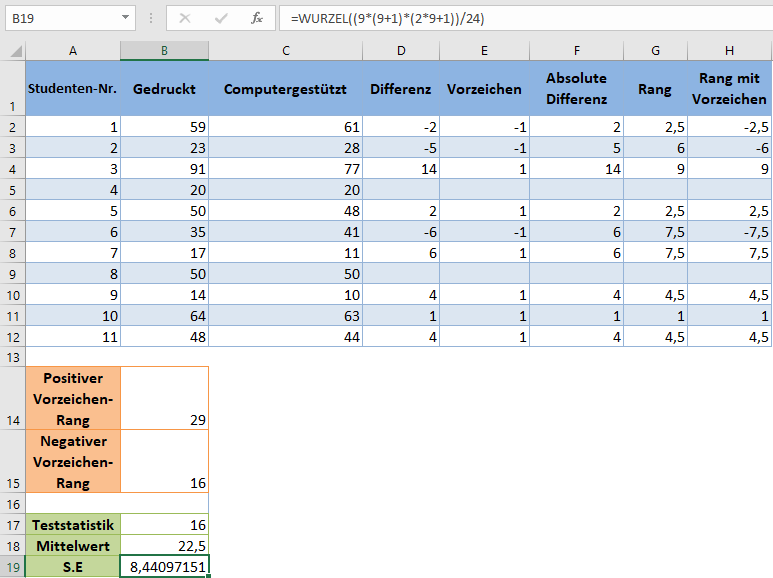
wobei n der Stichprobenumfang ist und der Standardfehler ist gegeben durch:
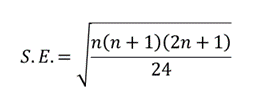
In unserem Fall ist n=9 nach Abzug der „Null“-Differenzen. Wir berechnen also den Mittelwert folgendermaßen:
und den Standardfehler folgendermaßen:
Berechnen Sie als Nächstes den t-Wert für die Beobachtungen mit Hilfe der folgenden Formel:
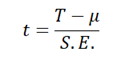
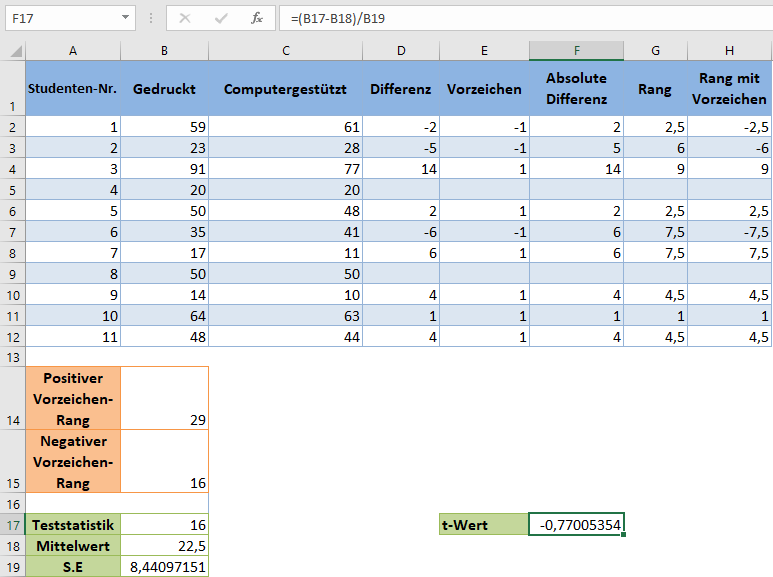
Berechnen Sie schließlich den p-Wert für die Beobachtungen mit der T.VERT-Funktion. Für die T.VERT-Funktion ist x der t-Wert, der Freiheitsgrad ist n-1=9-1=8 und für die kumulative Verteilungsfunktion wählen Sie ‚WAHR‘. Da wir einen zweiseitigen Test durchführen, multiplizieren wir das Ergebnis der T.VERT-Funktion mit 2.
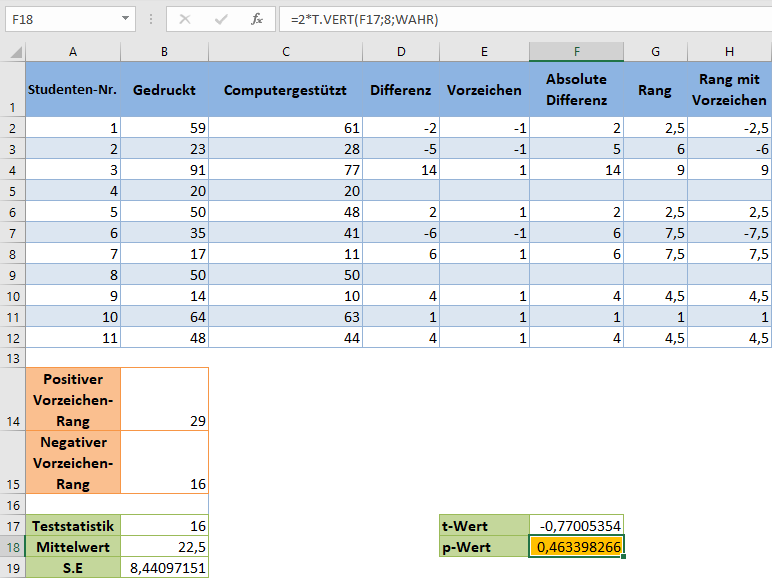
Der p-Wert beträgt hier 0,463, was über dem Signifikanzniveau von 5 % bzw. 0,05 liegt. Das bedeutet, dass wir zu dem Schluss kommen, dass es keinen statistisch signifikanten Beweis dafür gibt, dass die Art der Durchführung eines Tests die Testergebnisse der Studenten beeinflusst.
Der Wilcoxon-Vorzeichen-Rang-Test in Google Sheets
Der Wilcoxon-Vorzeichen-Rang-Test kann in Google Sheets auf ähnliche Weise wie in Excel (siehe unten) berechnet werden.
Für die Methode des kritischen Werts gilt Folgendes:
und bei Verwendung des p-Wertes haben wir:
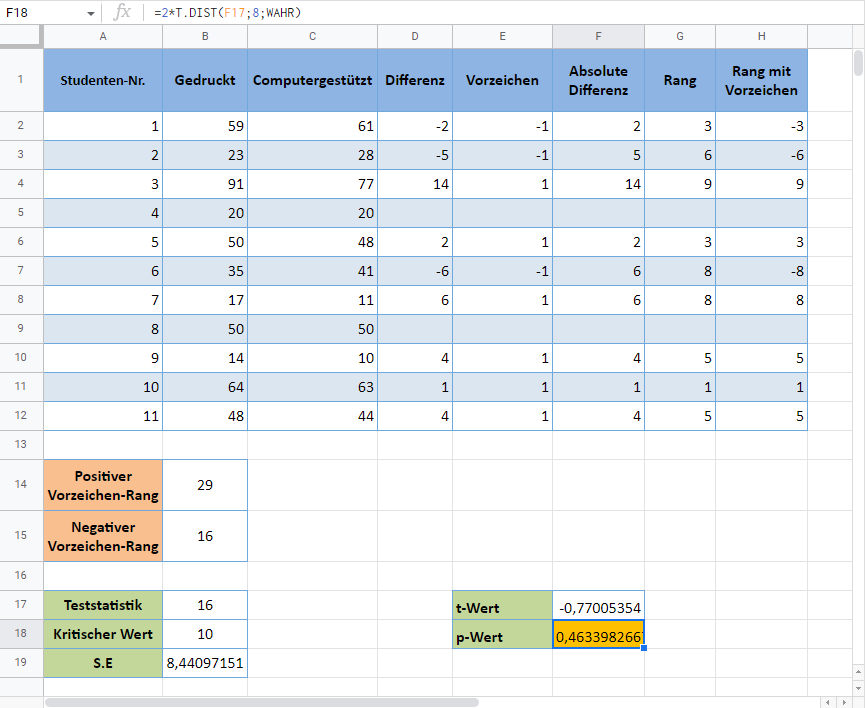
Hinweis: Die Excel-Funktion T.VERT behält ihre englische Bezeichnung (T.DIST) in der deutschen Version von Google Sheets, d. h. Sie erhalten einen Fehler, wenn Sie T.VERT in Google Sheets eingeben.