Wilcoxon-Rangsummentest (Mann-Whitney-U-Test) – Excel & GS
In diesem Tutorial zeigen wir Ihnen, wie Sie den Wilcoxon-Rangsummentest (Mann-Whitney-U-Test) in Excel und Google Sheets verwenden können.
Der Wilcoxon-Rangsummentest , auch Mann-Whitney-U-Test genannt, ist ein nicht parametrischer Test, der zum Vergleich der Mediane zwischen zwei Grundgesamtheiten verwendet wird. Mit anderen Worten: Er prüft, ob zwei Stichproben wahrscheinlich aus derselben Grundgesamtheiten stammen. Er erfüllt eine ähnliche Funktion wie der unabhängige t-Test für zwei Stichproben mit dem Unterschied, dass er im Gegensatz zum unabhängigen t-Test für zwei Stichproben keine Normalität der Grundgesamtheit voraussetzt.
Den unabhängigen t-Test für zwei Stichproben mit dem Wilcoxon-Rangsummentest vergleichen
- Sowohl der unabhängige T-Test für zwei Stichproben als auch der Wilcoxon-Rangsummentest werden verwendet, um festzustellen, ob ein statistisch signifikanter Unterschied zwischen ZWEI Gruppen von unabhängigen Stichproben besteht.
- Beim unabhängigen T-Test mit zwei Stichproben wird davon ausgegangen, dass der Datensatz aus einer normalverteilten Grundgesamtheit stammt, während diese Annahme beim Wilcoxon-Rangsummentest nicht gemacht wird.
Wann wird der Wilcoxon-Rangtest mit Vorzeichen verwendet?
Der Wilcoxon-Rangtest wird verwendet, wenn einer der Datensätze gegen die Normalitätsbedingung verstößt und die beiden Stichprobensätze unabhängig sind.
Annahmen für den Wilcoxon-Rangsummentest
- Die zu messenden Daten müssen sich auf der ordinalen oder kontinuierlichen Ebene befinden. (d. h. die Daten müssen eine Rangskala oder eine Zahl sein)
- Die Beobachtungen aus beiden Stichproben sind unabhängig voneinander.
Den Wilcoxon-Rangsummentest in Excel durchführen
Wilcoxon-Rangsummentest – Tabelle der kritischen Werte
Bei dieser Methode wird die Statistik des Wilcoxon-Rangsummentests mit dem kritischen Wert verglichen. Im Folgenden finden Sie eine schrittweise Anleitung zur Durchführung des Wilcoxon-Rangsummentests mit der Methode der kritischen Werte.
Beispiel
Hintergrund: Es wurde ein neues Medikament zur Behandlung von Kopfweh und Schmerzen hergestellt. Der Hersteller behauptet, das Medikament lindere Kopfschmerzen schneller als die derzeit auf dem Markt verfügbaren Medikamente. Ein Forscher möchte diese Behauptung testen und teilt daher Patienten mit starken Kopfschmerzen nach dem Zufallsprinzip in zwei Gruppen ein. Der einen Gruppe verabreichte er das neue Medikament und der anderen eines der gängigen älteren Medikamente. Er zeichnete die Zeit in Minuten auf, die jede Person benötigte, um ihre Kopfschmerzen zu lindern. Das Ergebnis ist in der nachstehenden Tabelle aufgeführt. Prüfen Sie auf einem Signifikanzniveau von 5 %, ob ein signifikanter Unterschied in der Zeit, die das neue Medikament und das alte Medikament zur Linderung der Kopfschmerzen benötigen, besteht.
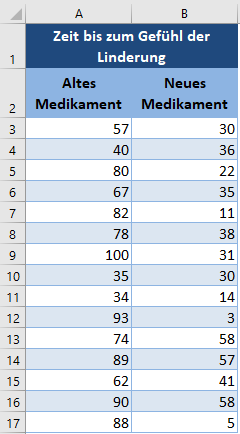
Weisen Sie zunächst jedem Datenpunkt (Zeit) einen Rang vom kleinsten bis zum größten mit der Funktion RANG.MITTELW zu:
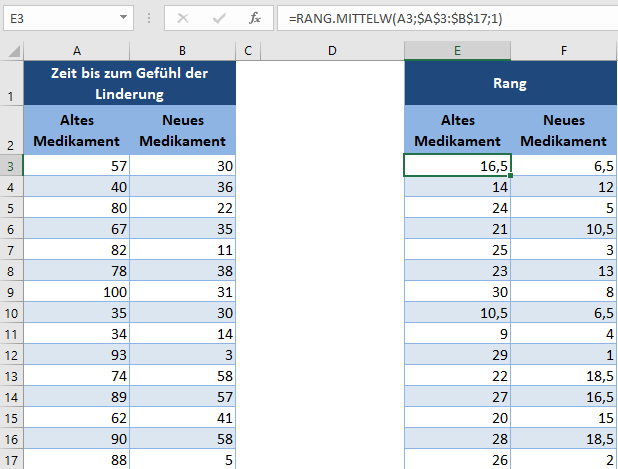
Beachten Sie, dass wir für den Bereich in der RANG.MITTELW-Funktion absolute Bezüge verwendet haben, damit wir die Formel problemlos in andere Zellen einfügen können, ohne den Bereich zu ändern.
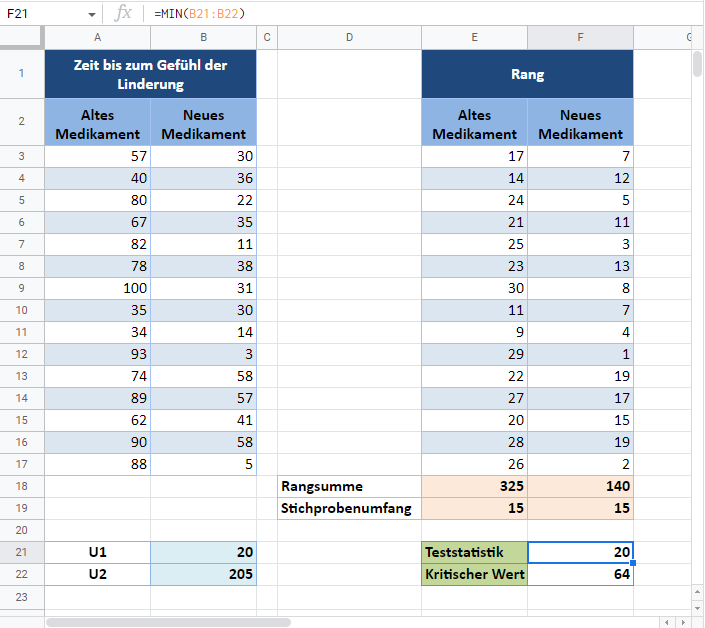
Als nächstes erhalten wir die Rangsumme für jede Gruppe (die Gruppe des alten Medikaments und die Gruppe des neuen Medikaments).
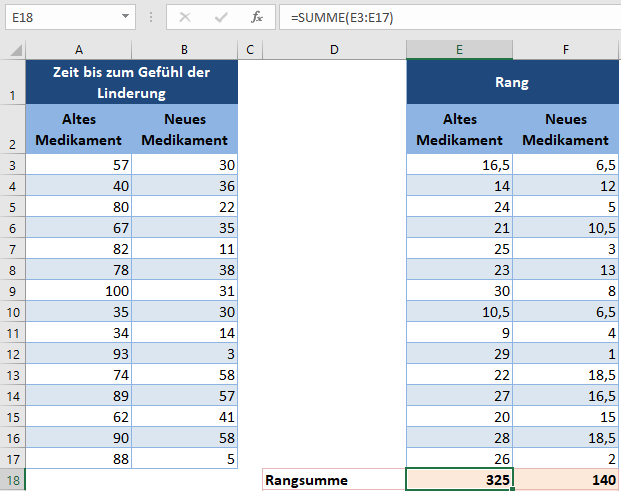
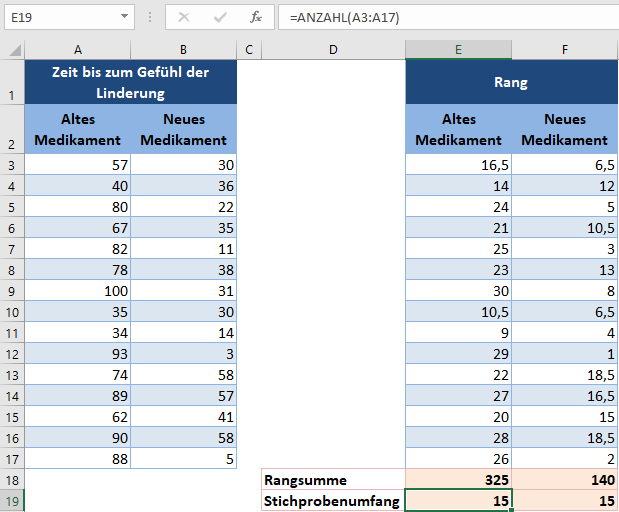
Verwenden Sie anschließend die ANZAHL-Funktion, um die Stichprobengrößen der beiden Gruppen zu ermitteln (siehe unten):
Die Teststatistik für den Wilcoxon-Rangsummentest wird mit U bezeichnet, was dem kleineren Wert von U1 und U2 entspricht. Diese sind folgendermaßen definiert:
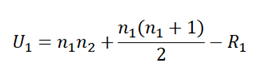
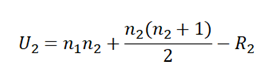
Dabei sind n1 und n2 die Stichprobengrößen von Gruppe 1 (Gruppe der alten Medikamente) und Gruppe 2 (Gruppe der neuen Medikamente), während R1 und R2 die Summen der Ränge von Gruppe 1 und Gruppe 2 entsprechen.
Als nächstes berechnen wir U1 und U2 wie folgt:
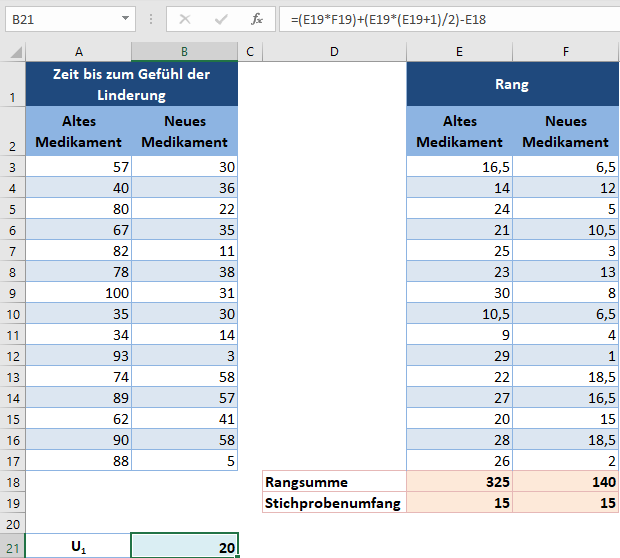
Ähnlich für U2:
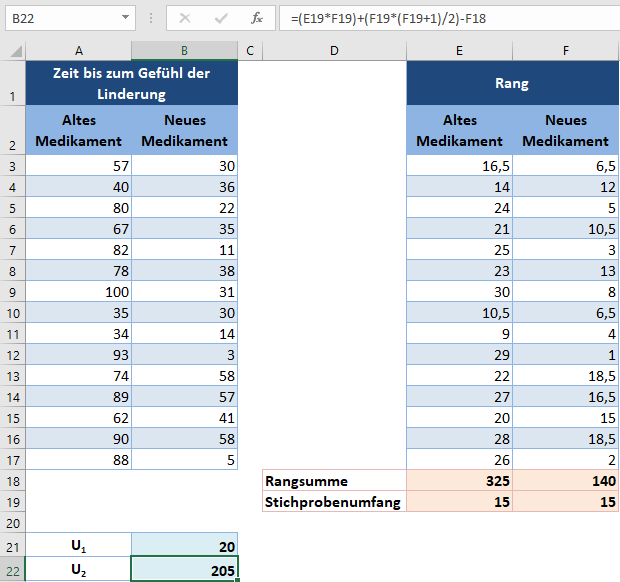
Die Teststatistik U ist der kleinere Wert von U1 und U2 und wird folgendermaßen berechnet:
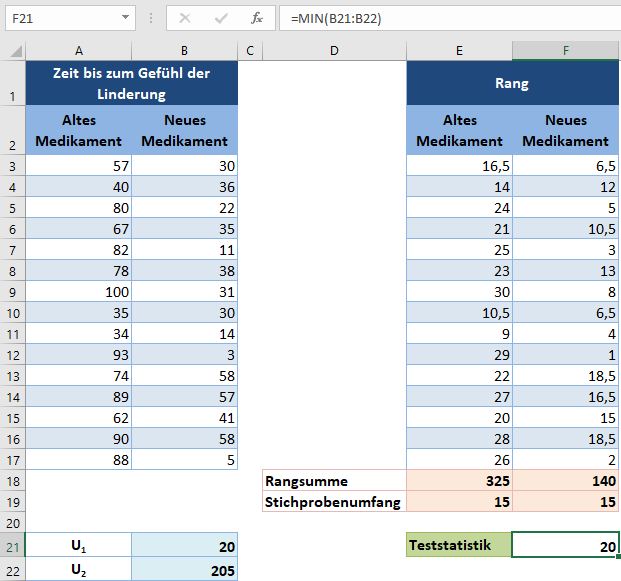
Der kritische Wert für den Stichprobenumfang n1= 15 und n2 =15 mit einem Signifikanzniveau von 5 % wird aus der Wilcoxon-Rangsummentabelle der kritischen Werte ermittelt.
Beachten Sie, dass wir hier einen zweiseitigen Test durchführen, da wir auf die Differenz der Werte testen (und nicht auf die Zunahme oder Abnahme der Werte), die in beide Richtungen geht, d. h. sowohl Zunahme als auch Abnahme der Werte.
Ein Auszug aus der Wilcoxon-Rangsummentabelle (Mann-Whitney-U) der kritischen Werte für einen zweiseitigen Test ist unten dargestellt:
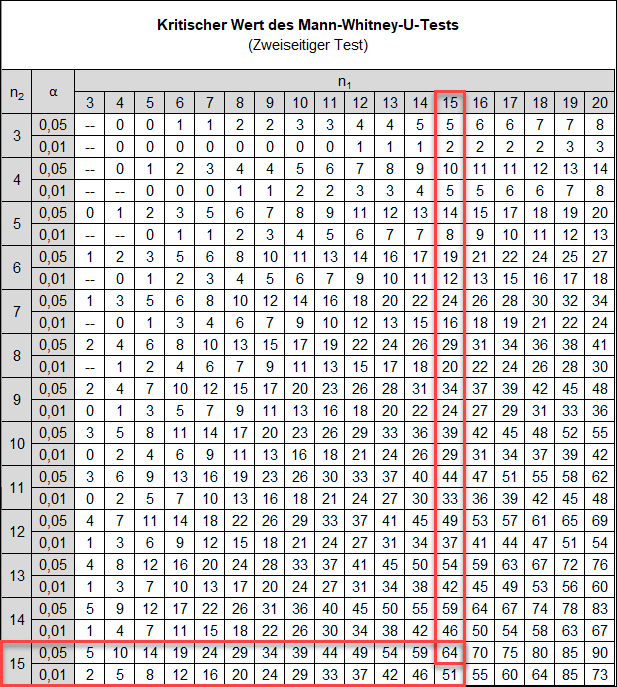
Der kritische Wert ist also 64.
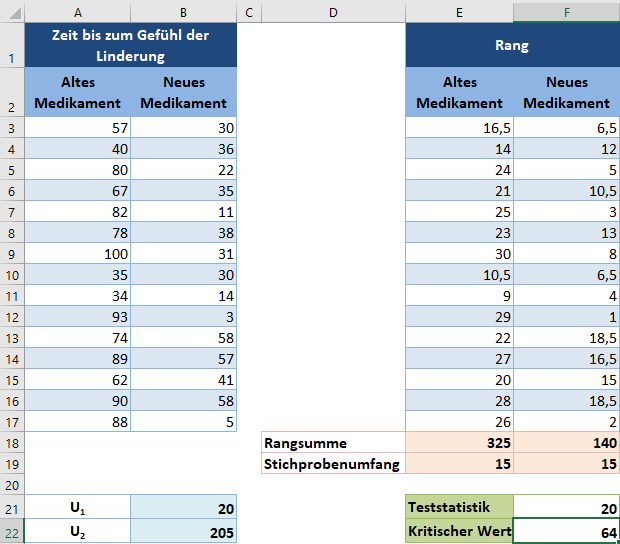
Beim Wilcoxon-Rangsummentest kommt man zu dem Schluss, dass ein signifikanter Unterschied zwischen den Gruppen besteht, wenn die Teststatistik kleiner als oder gleich dem kritischen Wert ist.
In diesem Fall ist die Teststatistik 20 und der kritische Wert 64. Da die Teststatistik kleiner als der kritische Wert ist, schließen wir, dass es statistisch signifikante Beweise dafür gibt, dass das neue Medikament die Kopfschmerzen schneller als das alte lindert.
Die p-Wert-Methode
Eine andere Methode zur Durchführung des Wilcoxon-Rangsummentests besteht darin, die Verteilung an eine Normalverteilung anzunähern und dann den p-Wert des angenäherten z-Wertes zu verwenden, um eine Aussage über die Grundgesamtheit der Gruppen zu treffen.
In den folgenden Schritten wird diese Methode anhand des gleichen Beispiels wie bei der vorherigen Methode veranschaulicht.
Beispiel
Hintergrund: Es wurde ein neues Medikament zur Behandlung von Kopfweh und Schmerzen hergestellt. Der Hersteller behauptet, das Medikament lindere Kopfschmerzen schneller als die derzeit auf dem Markt verfügbaren Medikamente. Ein Forscher möchte diese Behauptung testen und teilt daher Patienten mit starken Kopfschmerzen nach dem Zufallsprinzip in zwei Gruppen ein. Der einen Gruppe verabreichte er das neue Medikament und der anderen eines der gängigen älteren Medikamente. Er zeichnete die Zeit in Minuten auf, die jede Person benötigte, um ihre Kopfschmerzen zu lindern. Das Ergebnis ist in der nachstehenden Tabelle aufgeführt. Prüfen Sie auf einem Signifikanzniveau von 5 %, ob ein signifikanter Unterschied in der Zeit, die das neue Medikament und das alte Medikament zur Linderung der Kopfschmerzen benötigen, besteht.
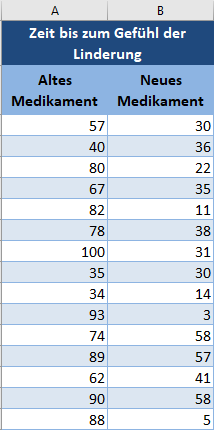
Wir werden alle in der vorherigen Methode beschriebenen Schritte durchführen, um die Summe der Ränge der beiden Gruppen und die Stichprobengrößen zu erhalten.
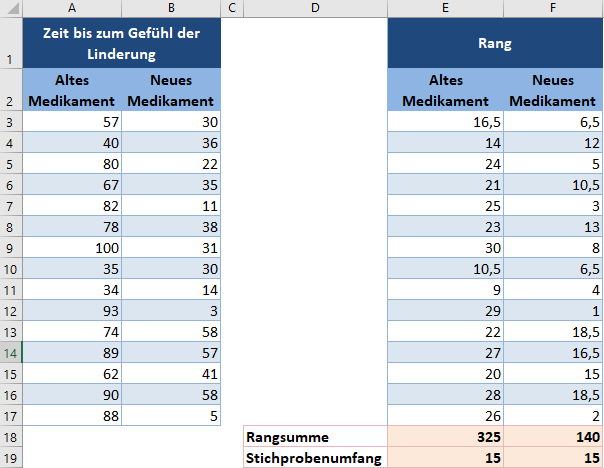
Bei dieser Methode entspricht die Teststatistik T der kleineren der Rangsummen der beiden Gruppen. Diese ergibt sich wie folgt:
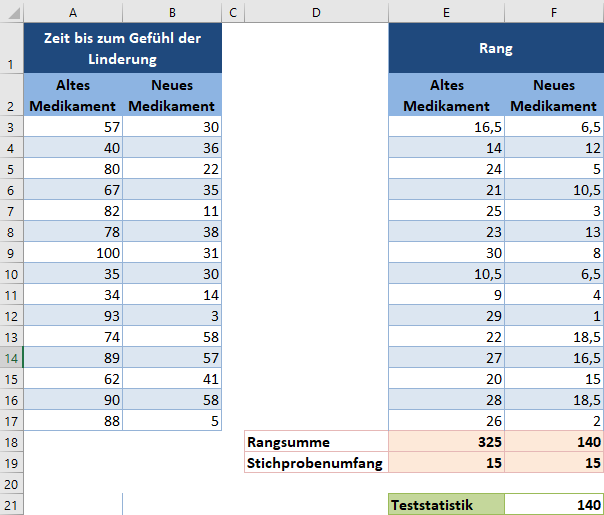
Nun erhalten wir den Mittelwert und den Standardfehler der Verteilung. Der Mittelwert (μ) der Verteilung ist gegeben durch:
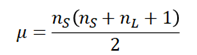
wobei nS und nL die Stichprobenumfänge der kleineren und der größeren Rangsummengruppe sind und der Standardfehler durch die folgende Formel gegeben ist:
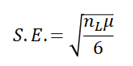
Dies ist äquivalent zu:
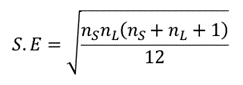
In unserem Fall ist nS = nL = 15. Wir berechnen also den Mittelwert wie folgt:
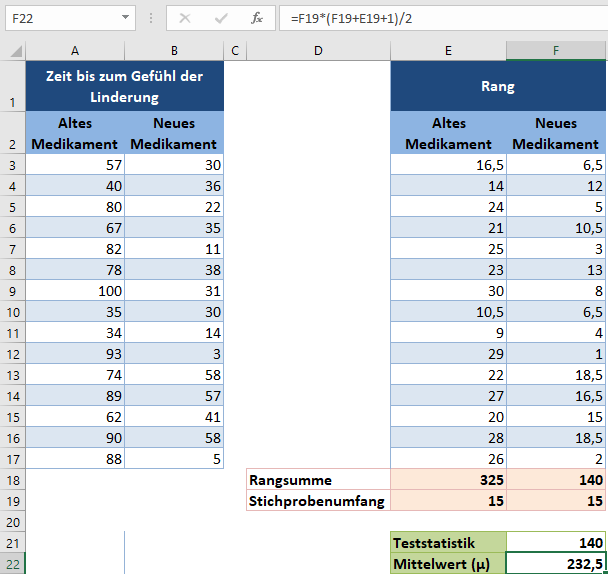
und den Standardfehler wie folgt:
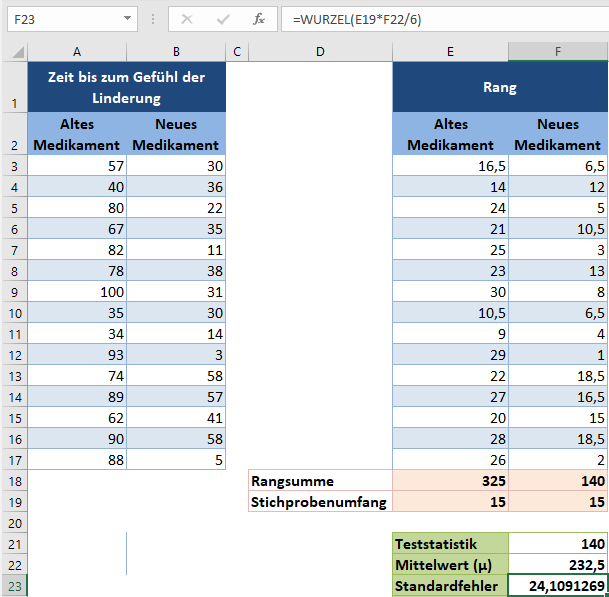
Berechnen Sie als nächstes den z-Wert für die Beobachtungen mit Hilfe der Formel:
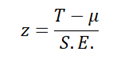
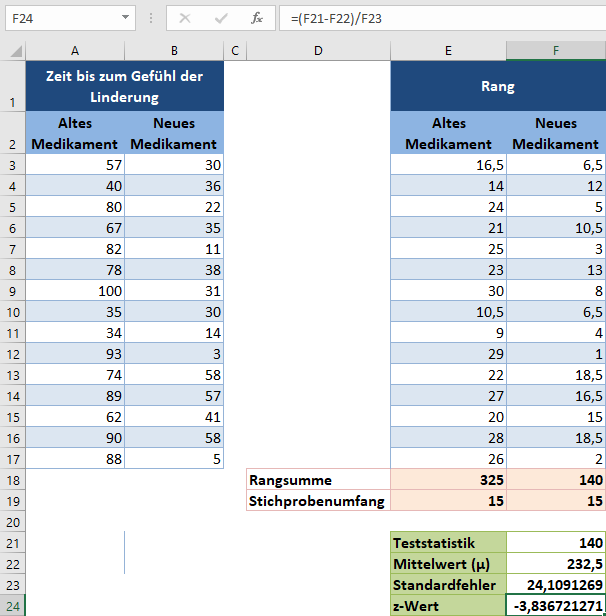
Berechnen Sie abschließend den p-Wert für die Beobachtungen mit Hilfe der NORM.VERT- oder NORM.S.VERT-Funktion. Da wir einen zweiseitigen Test durchführen, multiplizieren wir das Ergebnis der Funktionen NORM.VERT oder NORM.S.VERT mit 2.
Die NORM.VERT-Funktion hat die folgende Syntax: NORM.VERT(x, Mittelwert, Standabwn, Kumuliert), wobei:
- x = die Teststatistik
- Mittelwert = der aus den Daten berechnete Mittelwert
- Standabwn = Standardfehler
und bei „Kumuliert“ wählen Sie „TRUE“ für die kumulative Verteilungsfunktion aus.
Die NORM.S.VERT-Funktion hat die folgende Syntax: NORM.S.VERT(z, Kumuliert), wobei z der z-Score ist. Bei „Kumuliert“ wählen Sie „TRUE“ für die kumulative Verteilungsfunktion aus.
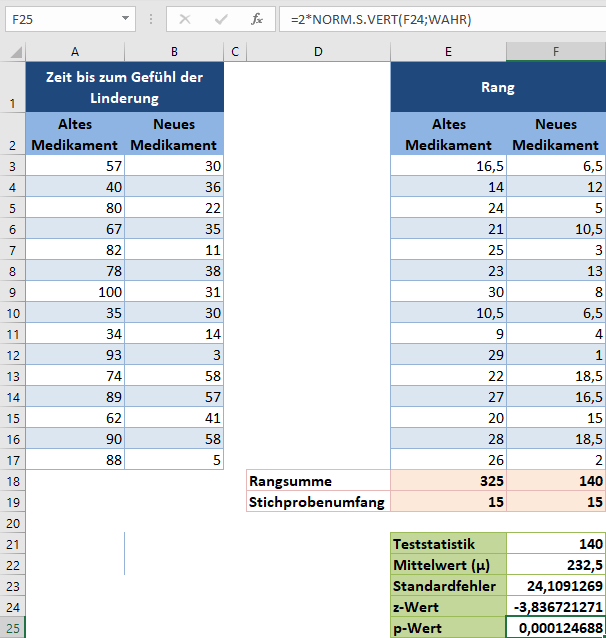
Der p-Wert ist hier kleiner als unser Signifikanzniveau von 5% oder 0,05. Das bedeutet, dass wir zu dem Schluss kommen, dass es statistisch signifikante Beweise dafür gibt, dass das neue Medikament die Kopfschmerzen schneller als das alte lindert.
Der Wilcoxon-Rangtest mit Vorzeichen in Google Sheets
Der Wilcoxon Rangtest mit Vorzeichen kann in Google Sheets auf ähnliche Weise wie in Excel berechnet werden (siehe unten).
Für die Methode des kritischen Wertes gilt Folgendes: