Vertrauensintervalle in Excel und Google Sheets

In diesem Tutorial zeigen wir Ihnen, wie Sie Konfidenzintervalle in Excel und Google Sheets erstellen können.

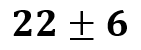Konfidenzintervalle (KIs) geben den Wertebereich an, in den der tatsächliche Mittelwert (der Durchschnitt) für eine Population fallen sollte. Sie werden in der Regel wie folgt angezeigt:Dies bedeutet, dass wir bei einem bestimmten Konfidenzniveau erwarten, dass der tatsächliche Mittelwert der Population innerhalb von 6 Einheiten unter und über 22 fällt. Konfidenzintervalle werden auf der Grundlage eines Stichprobenmittelwerts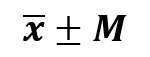 aus der Grundgesamtheit berechnet, wobei ein „Konfidenzniveau“ verwendet wird. So bietet beispielsweise ein Konfidenzniveau von 99% eine größere Sicherheit als ein Konfidenzniveau von 90%, dass der tatsächliche Mittelwert innerhalb des Konfidenzintervalls liegt.

Die Fehlermarge (F) gibt an, wie weit über und unter dem Stichprobenmittelwert die obere bzw. untere Grenze des Konfidenzintervalls liegt. Nach der Berechnung der Fehlermarge wird das Konfidenzintervall als Stichprobenmittelwert (Durchschnitt) und Fehlermarge mit einem Plus-Minus-Zeichen (±) dazwischen dargestellt:

Konfidenzintervalle in Excel berechnen

Es gibt drei Möglichkeiten, Konfidenzintervalle in Excel zu berechnen:

1. Die Funktionen KONFIDENZ.NORM oder KONFIDENZ.T.
2. Die Option Populationskenngrößen der Schaltfläche Datenanalyse auf der Hauptregisterkarte Daten
3. Manuelles Berechnen des Konfidenzintervalls.

KONFIDENZ-Funktionen

Die Funktionen KONFIDENZ.NORM und KONFIDENZ.T geben den zur Berechnung des Konfidenzintervalls verwendeten Fehlerspielraum zurück.

Wann sollte man KONFIDENZ.NORM oder KONFIDENZ.T verwenden?

• Die Funktion .NORM wird verwendet, wenn die Standardabweichung der Grundgesamtheit bekannt ist.
• Die Funktion .T wird verwendet, wenn die Standardabweichung der Grundgesamtheit unbekannt ist.

Gemäß dem Zentralen Grenzwertsatz (ZGS), einem leistungsstarken Statistiksatz, kann jedoch die Standardabweichung der Stichprobe zur Annäherung an die Standardabweichung der Grundgesamtheit verwendet werden, wenn die Stichprobe ausreichend groß ist (normalerweise 30 oder mehr).

Mit anderen Worten: Verwenden Sie die Funktion KONFIDENZ.NORM, wenn die Standardabweichung der Grundgesamtheit bekannt ist oder wenn die Standardabweichung der Grundgesamtheit unbekannt ist, aber der Stichprobenumfang 30 oder mehr beträgt.

Syntax von Konfidenzfunktionen

=KONFIDENZ.NORM(Alpha; Standardabweichung; Stichprobenumfang)

=KONFIDENZ.T(Alpha; Standardabweichung; Stichprobenumfang)

Alpha ist das Signifikanzniveau, das sich durch Subtraktion des Konfidenzniveaus von 1 ergibt. Angenommen, Sie möchten das Konfidenzintervall des Mittelwerts mit einem Konfidenzniveau von 95% berechnen, so entspricht das Signifikanzniveau (Alpha) 1-0,95 = 0,05. Die gebräuchlichsten Konfidenzniveaus zur Berechnung von Konfidenzintervallen sind 90%, 95% und 99%.

Beispiel für KONFIDENZ.NORM

Hintergrund: Es wird angenommen, dass die Zeit in Minuten, um einen Marathon zu beenden, normalverteilt ist. Eine Zufallsstichprobe von Marathonläufern wurde beobachtet und die Zeit, die sie brauchten, um einen Marathon zu beenden, wird unten dargestellt. Berechnen wir ein 95%-Konfidenzintervall für die mittlere (durchschnittliche) Zeit, die alle Läufer für einen Marathon benötigen.

Berechnen Sie zunächst den Stichprobenmittelwert (Durchschnitt) der Stichprobe mithilfe der MITTELWERT-Funktion.

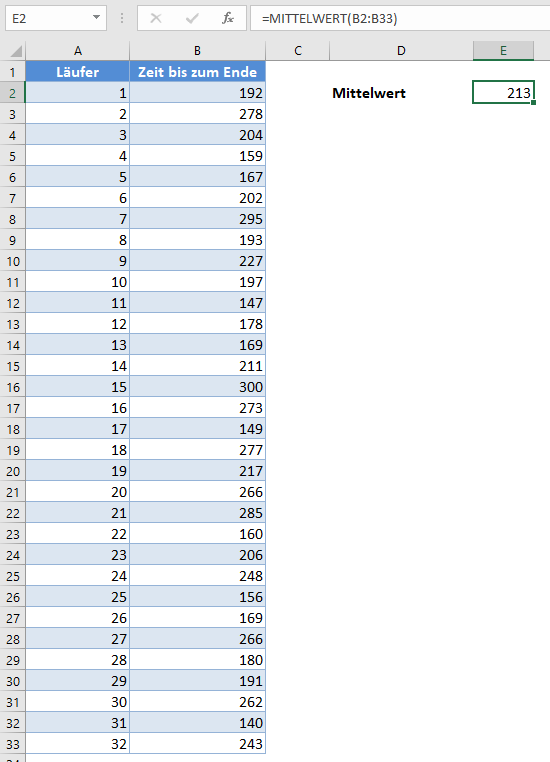
Berechnen Sie anschließend die Standardabweichung (SA) der Stichprobe mit der STABW.S-Funktion.

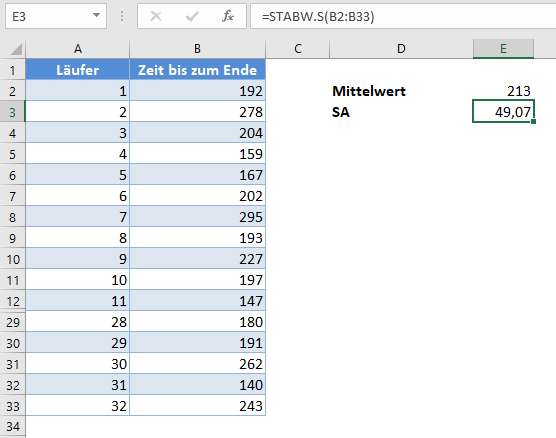
Hinweis: Die STABW.S-Funktion wird zur Berechnung der Standardabweichung der Stichprobe verwendet, während STABW.N zur Berechnung der Standardabweichung der Grundgesamtheit verwendet wird. Verwenden Sie bei der Berechnung von Konfidenzintervallen immer die Funktion STABW.S, um die Standardabweichung der Stichprobe zu berechnen.

Berechnen Sie anschließend den Stichprobenumfang mit der ANZAHL-Funktion.

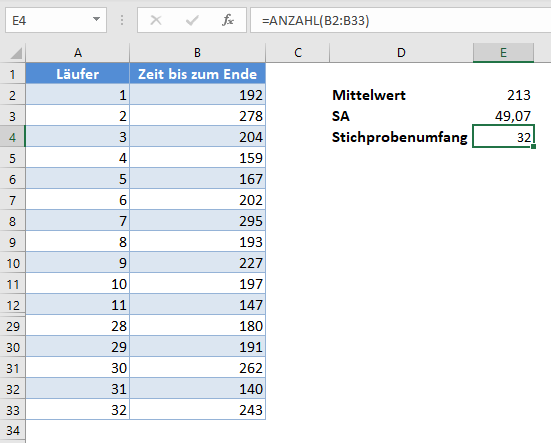
Zur Berechnung eines Konfidenzintervalls von 95 % beträgt das Alpha (Signifikanzniveau) 1-0,95 = 0,05.

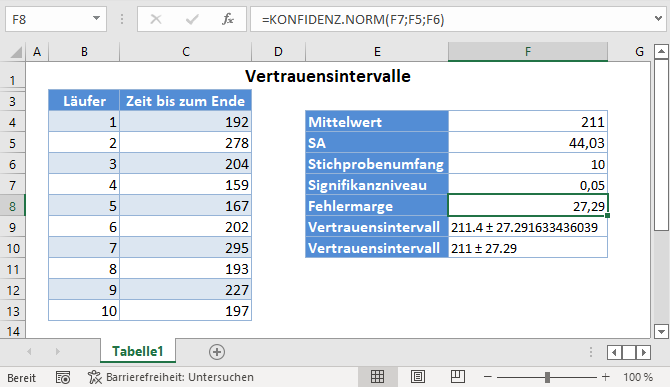
Berechnen Sie nun die Fehlermarge mit der KONFIDENZ.NORM-Funktion.

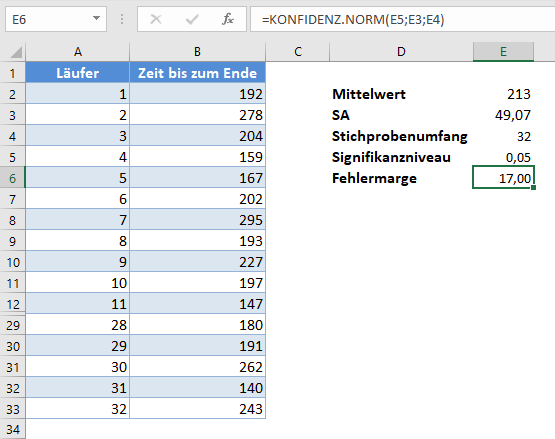
Hinweis: Wir verwenden hier die KONFIDENZ.NORM-Funktion, da wir gemäß dem zentralen Grenzwertsatz (ZGS) die Standardabweichung der Grundgesamtheit anhand der Standardabweichung der Stichprobe annähern können, wenn der Stichprobenumfang 30 oder mehr beträgt.

Verwenden Sie die VERKETTEN-Funktion, um das Konfidenzintervall durch Addieren und Subtrahieren der Fehlermarge vom Mittelwert anzuzeigen.

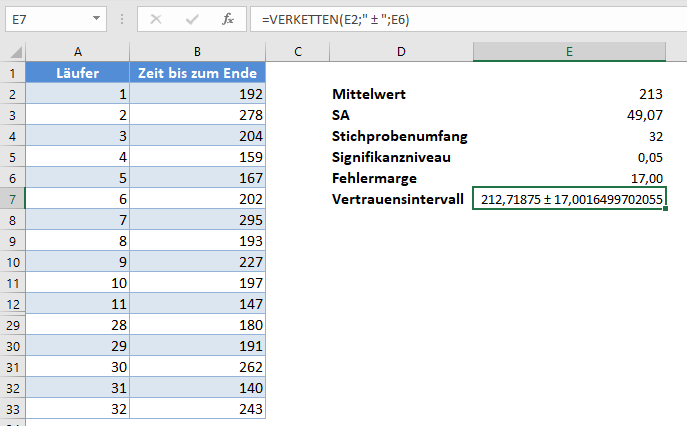
Hinweis: Die VERKETTEN-Funktion rundet die Werte nicht. Fügen wir also die RUNDEN-Funktion in die Formel ein, um das Ergebnis besser lesbar zu machen.

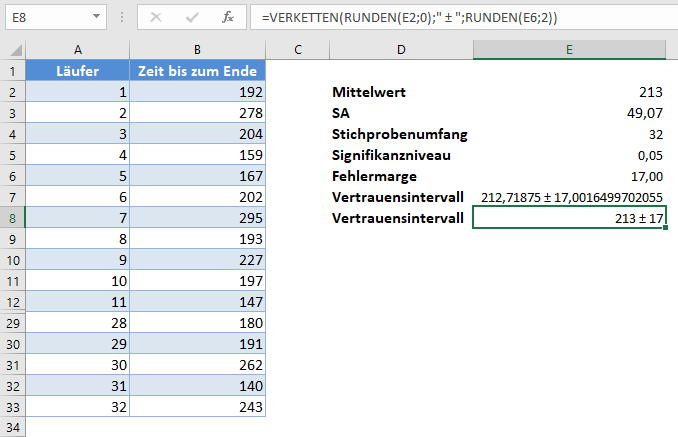
Unser Konfidenzintervall für den Mittelwert der Grundgesamtheit ist 213±17 oder einfach (196 , 230).

Beispiel für KONFIDENZ.T

Hintergrund: Es wird angenommen, dass der Intelligenzquotient von College-Studenten in den Vereinigten Staaten einer Normalverteilung folgt. Die Intelligenzquotienten einer Zufallsstichprobe von 5 US-College-Studenten sind wie unten dargestellt. Berechnen wir ein 99%-Konfidenzintervall für den mittleren (durchschnittlichen) Intelligenzquotienten aller Hochschulstudenten in den Vereinigten Staaten.

In diesem Fall ist Alpha (Signifikanzniveau) 1-0,99 = 0,01.

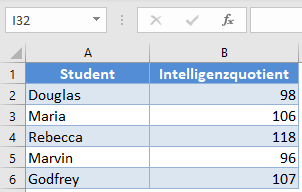
Führen Sie die Schritte im vorherigen Beispiel aus, um den Mittelwert, die Standardabweichung (SA) und den Stichprobenumfang zu berechnen.

Berechnen Sie nun die Fehlermarge mithilfe der KONFIDENZ.T-Funktion in Excel.

Hinweis: Wir haben hier die KONFIDENZ.T-Funktion verwendet, weil wir die Standardabweichung der Grundgesamtheit nicht kennen und der Stichprobenumfang klein ist (weniger als 30).

Das Konfidenzintervall für den Populationsmittelwert beträgt 105±17,95 oder einfach (87,05 , 122,95).

Konfidenzintervalle mit Populationskenngrößen berechnen

Eine weitere alternative Methode zur Berechnung von Konfidenzintervallen in Excel ist die Verwendung der Funktion Populationskenngrößen. Diese Funktion befindet sich in der Hauptregisterkarte Daten > Datenanalyse.

Wenn Sie die Option Datenanalyse nicht sehen, müssen Sie das Datenanalyse-Toolpak installieren.

Wählen Sie im Fenster Datenanalyse die Option Populationskenngrößen und klicken Sie auf OK.

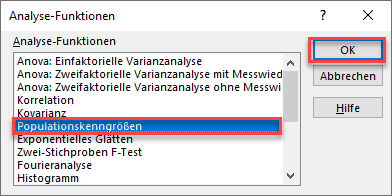
Als nächstes müssen Sie die Parameter konfigurieren.

• Klicken Sie auf „Eingabebereich“ und wählen Sie die Zellen aus, die die Quelldaten enthalten.
• Wählen Sie im Abschnitt „Geordnet nach“ das Optionsfeld „Spalten“.
• Aktivieren Sie das Kontrollkästchen „Beschriftungen in erster Zeile“, wenn der ausgewählte Bereich Spaltenüberschriften enthält, wie im folgenden Beispiel gezeigt.
• Wählen Sie die gewünschte Ausgabeoption. Um die Ergebnisse auf demselben Blatt zu erhalten, wählen Sie den Ausgabebereich und geben Sie den spezifischen Verweis auf die Zelle an, in der die Matrix angezeigt werden soll. In unserem Fall ist es $D$2.
• Aktivieren Sie das Kontrollkästchen „Konfidenzniveau für Mittelwert“ und geben Sie das gewünschte Konfidenzniveau ein (in unserem Fall 95% für Beispiel 1 und 99% für Beispiel 2).
• Sie können auch die anderen Kontrollkästchen ankreuzen, um weitere deskriptive Statistikwerte für die Daten zu erhalten (einschließlich der Kontrollkästchen „Statistische Kenngrößen“, „K-größter Wert“ und „K-kleinster Wert“).

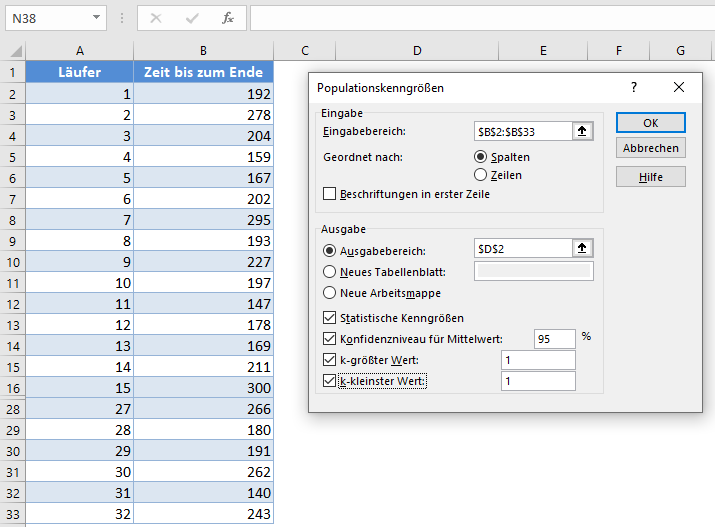
Die Ausgabe für das erste Beispiel sieht wie folgt aus:

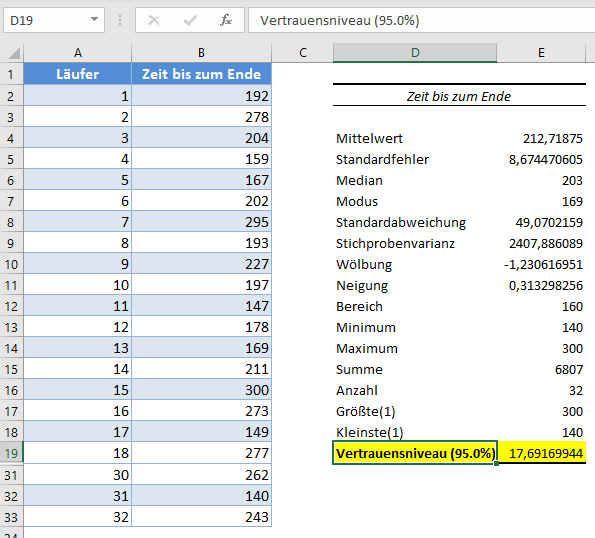
Aus dem obigen Ergebnis geht hervor, dass der Konfidenzwert (Fehlermarge) ungefähr 17,69 beträgt. Um das Konfidenzintervall zu erhalten, addieren und subtrahieren wir den Konfidenzwert vom Mittelwert wie folgt: 213±17,69, was einem Konfidenzintervall von (195,31 , 230,69) entspricht .

Konfidenzintervallformel in Excel

Sie können Konfidenzintervalle auch berechnen, indem Sie die Konfidenzintervallformel direkt verwenden. Die Formel für das 100(1-α)%-Konfidenzintervall lautet wie folgt:

Mittelwert ± z_krit (oder t_krit) * (Standardabweichung / Quadratwurzel des Stichprobenumfangs)

z_krit (oder t_krit) * (Standardabweichung / Quadratwurzel des Stichprobenumfangs) ist die Fehlermarge.

• Verwenden Sie z_krit, wenn die Standardabweichung der Grundgesamtheit bekannt ist.
• Verwenden Sie t_krit, wenn die Standardabweichung der Grundgesamtheit unbekannt ist.
• Verwenden Sie z_krit, wenn die Standardabweichung der Grundgesamtheit unbekannt ist, aber die Stichprobe 30 oder mehr beträgt.

Excel verfügt nicht über eine spezielle Funktion zur Ermittlung des z_krit für ein bestimmtes Konfidenzniveau. Für t_krit gibt es jedoch die Funktion T.INV.2S, die den t_krit für ein bestimmtes Konfidenzniveau und einen bestimmten Freiheitsgrad liefert. Wir werden diese Funktion in Beispiel 2 näher erläutern. Für die gängigen Konfidenzniveaus 90%, 95% und 99% beträgt der z_krit 1,645, 1,96 bzw. 2,576.

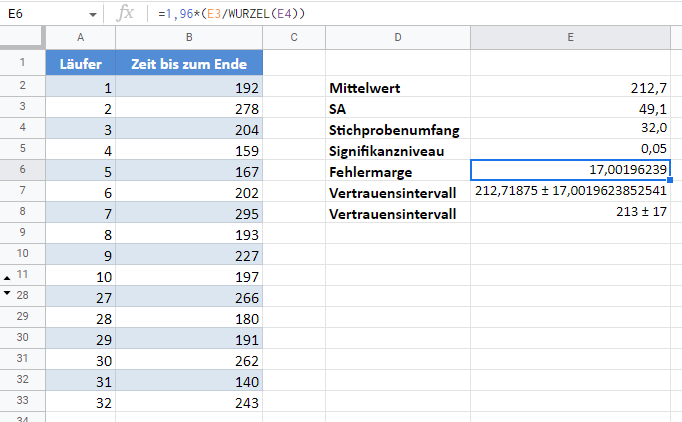
Für Beispiel 1 werden wir 1,96 als z_krit für unser 95%-Konfidenzintervall verwenden. Das Verfahren wird im Folgenden dargestellt:

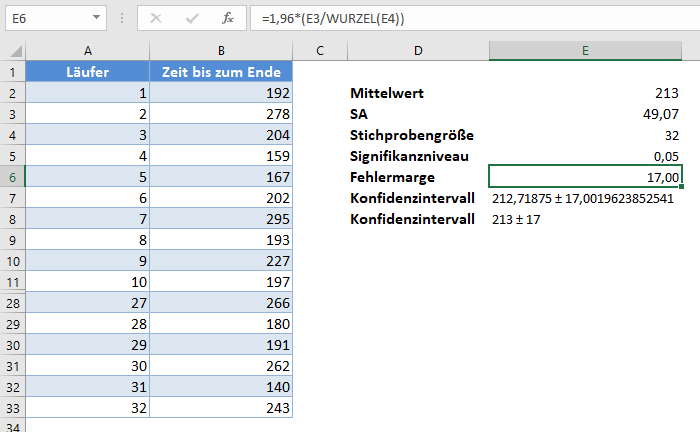
Die Fehlermarge ergibt 17,00 und wie üblich ist das Konfidenzintervall Mittelwert ± Fehlermarge, was 213±17 oder (213-17,213+17)=(196,230) entspricht.

Für Beispiel 2 wird die Funktion T.INV.2T verwendet, um den t_krit des 99%-Konfidenzintervalls zu erhalten, da die Standardabweichung der Grundgesamtheit unbekannt und die Stichprobe klein ist. Die Funktion T.INV.2S benötigt zwei Argumente: Wahrscheinlichkeit (Alpha) und Freiheitsgrad. Bei der Ermittlung von Konfidenzintervallen dient Alpha als Wahrscheinlichkeit. Den Freiheitsgrad (FG) erhält man, indem man 1 vom Stichprobenumfang subtrahiert. In unserem Fall also FG = 5 – 1 = 4.

Wir gehen also wie folgt vor, um Konfidenzintervalle direkt zu berechnen, wenn die Standardabweichung der Grundgesamtheit unbekannt und die Stichprobe klein ist.

Verwenden Sie zunächst die in den vorherigen Beispielen beschriebenen Methoden zur Berechnung von Mittelwert, Standardabweichung, Stichprobenumfang und Signifikanzniveau. Anschließend erhalten Sie den Freiheitsgrad.

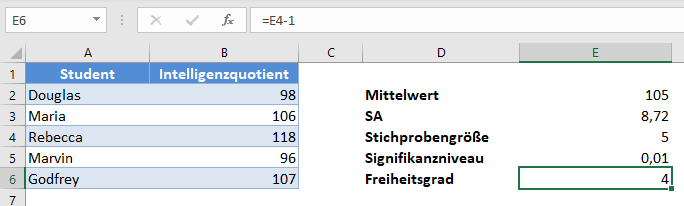
Anschließend erhalten Sie den kritischen Wert (t_krit).

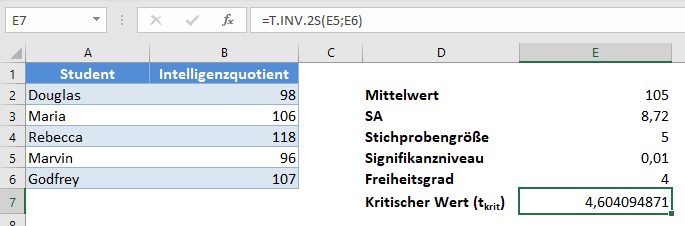
Berechnen Sie nun die Fehlermarge.

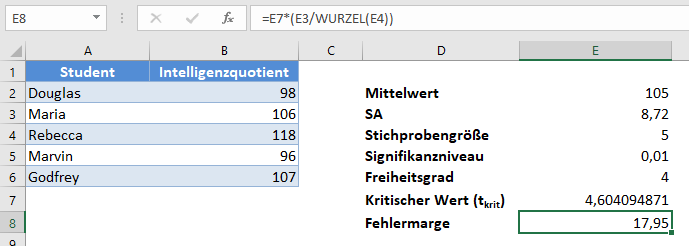
Stellen Sie schließlich das Konfidenzintervall dar.

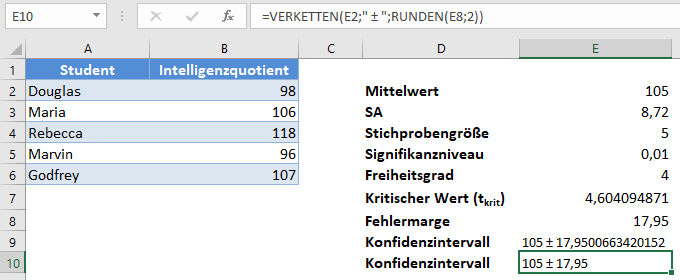
Die Fehlermarge beträgt 17,95 und wie üblich ist das Konfidenzintervall Mittelwert ± Fehlermarge, also 105±17,95 oder (105-17,95,105+17,95)=(87,05,122,95).

Konfidenzintervalle in Google Sheets

Konfidenzintervalle können mit ähnlichen Methoden in Google Sheets berechnet werden.

Sie können die Funktionen KONFIDENZ.NORM und KONFIDENZ.T verwenden.

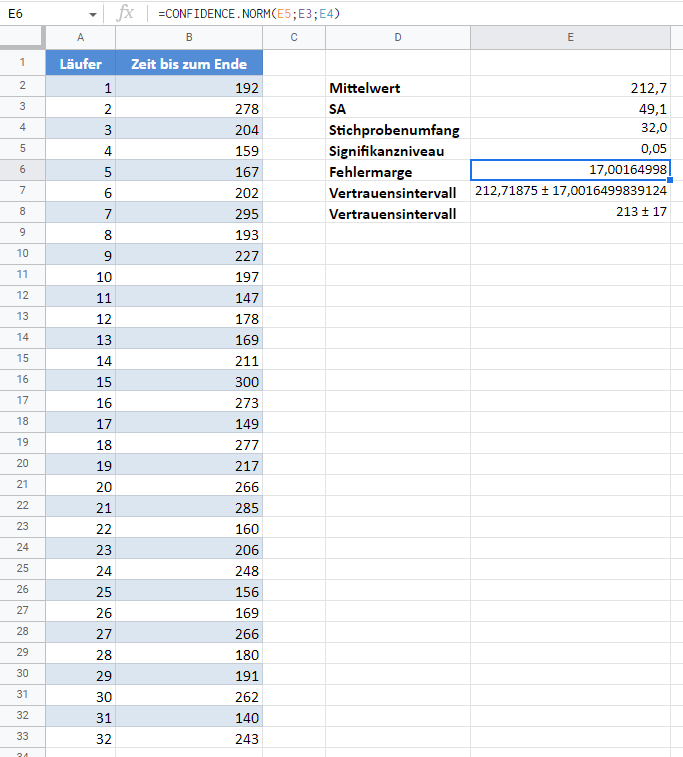
Oder Sie können das Konfidenzintervall manuell berechnen:

Konfidenzintervall – XLMiner-Analyse-Toolpak

Google Sheets verfügt nicht über das Datenanalyse-Toolpak, sondern über das Add-on XLMiner Analysis Toolpak.

Nachdem Sie dieses Add-on installiert haben, finden Sie es auf der Registerkarte Erweiterungen . Wählen Sie XLMiner Analysis ToolPak und klicken Sie auf Start.

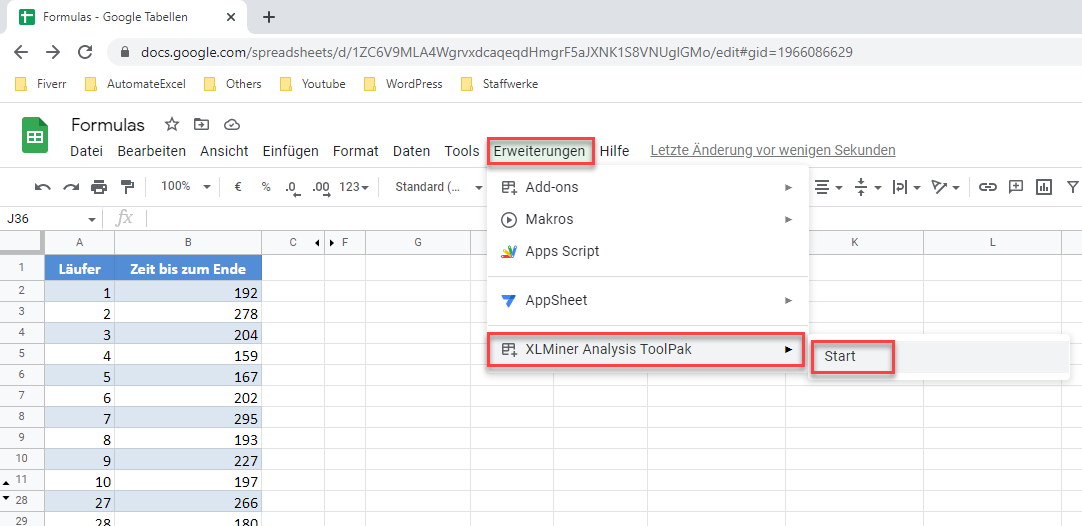
Im XLMiner-Analysis-ToolPak-Fenster wählen Sie Descriptive Statistics.

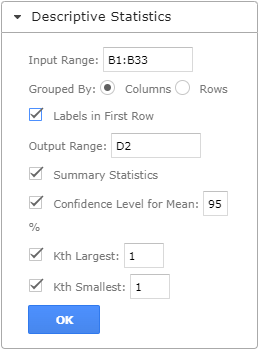
Im Dropdown-Menü der Option Descriptive Statistics konfigurieren Sie die Parameter wie folgt.

• Wählen Sie die Zellen aus, die die Quelldaten enthalten, und klicken Sie auf das Feld „Input Range“.
• Wählen Sie im Abschnitt „Grouped By“ das Optionsfeld „Columns“.
• Aktivieren Sie das Kontrollkästchen „Labels in First Row“ wie im folgenden Beispiel gezeigt, wenn der ausgewählte Bereich Spaltenüberschriften enthält.
• Geben Sie die gewünschte Startzelle oder den Startbereich für die Ausgabe in das Feld „Output Range“ ein.
• Aktivieren Sie das Kontrollkästchen „Confidence Level for Mean“ und geben Sie das gewünschte Konfidenzniveau ein, was in unserem Fall 95% ist.
• Sie können auch die anderen Kontrollkästchen ankreuzen, um weitere deskriptive Statistikwerte für die Daten zu erhalten (einschließlich der Kontrollkästchen „Summary Statistics“, „Kth Largest“ und „Kth Smallest“).
• Klicken Sie dann auf „OK“.

Die Ausgabe lautet wie folgt:

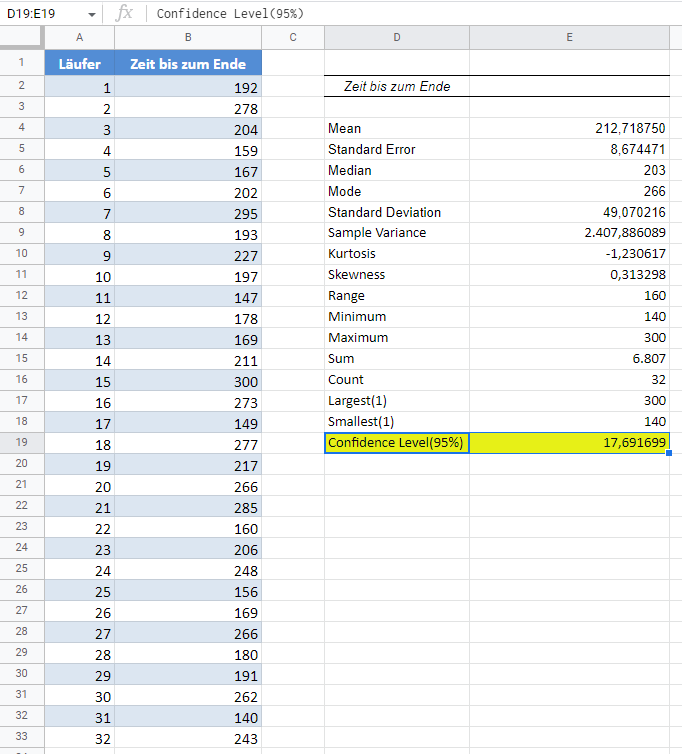
Aus dem obigen Ergebnis ergibt sich ein Konfidenzwert (Fehlermarge) von etwa 17,69. Um das Konfidenzintervall von zu erhalten, addieren und subtrahieren wir den Konfidenzwert vom Mittelwert wie gezeigt: 213±17,69, was dem Konfidenzintervall (195,31 , 230,69) entspricht.