Test von Shapiro Wilk – Excel und Google Sheets
In diesem Tutorial zeigen wir Ihnen, wie Sie den Shapiro-Wilk-Test in Excel und Google Sheets durchführen können.
Der Shapiro-Wilk-Test ist ein statistischer Test, der durchgeführt wird, um festzustellen, ob ein Datensatz mit Hilfe der Normalverteilung modelliert werden und somit eine zufällig ausgewählte Teilmenge des Datensatzes als normalverteilt angesehen werden kann. Der Shapiro-Wilk-Test gilt aufgrund seiner hohen statistischen Aussagekraft als eine der besten numerischen Methoden zur Überprüfung der Normalität.
Der ursprüngliche Shapiro-Wilk-Test hängt, wie die meisten Signifikanzprüfungen, vom Stichprobenumfang ab und funktioniert am besten bei Stichprobengrößen von n=2 bis n=50. Für größere Stichprobengrößen (bis zu n=2000) kann eine Erweiterung des Shapiro-Wilk-Tests, und zwar der Shapiro-Wilk-Royston-Test verwendet werden.
Wie der Shapiro-Wilk-Test funktioniert
Der Shapiro-Wilk-Test prüft die Nullhypothese, dass der Datensatz aus einer normalverteilten Grundgesamtheit stammt gegen die Alternativhypothese, dass der Datensatz nicht aus einer normalverteilten Grundgesamtheit stammt.
Die Teststatistiken für den Shapiro-Wilk-Test lauten wie folgt: 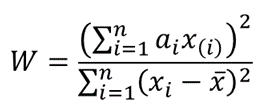
dabei ist x(i) die i-te Ordnungsstatistik (d. h. der i-te Datenwert, nachdem der Datensatz in aufsteigender Reihenfolge angeordnet wurde),
![]() ist der Mittelwert (Durchschnitt) des Datensatzes.
ist der Mittelwert (Durchschnitt) des Datensatzes.
n ist die Anzahl der Datenpunkte im Datensatz und
a = [ai] = (a1,…,an ) ist der Koeffizientenvektor der Gewichte des Shapiro-Wilk-Tests (aus der Shapiro-Wilk-Testtabelle),
Der Vektor a ist antisymmetrisch, d. h. a n+1-i =-ai für alle i, und a(n+1)/2 = 0 für ungerade n. Außerdem ist aT a = 1.
Der p-Wert ergibt sich aus dem Vergleich der W-Statistik mit den W-Werten, die in der Shapiro-Wilk-Testtabelle der p-Werte für den gegebenen Stichprobenumfang angegeben sind.
- Ist der erhaltene Wert kleiner als das gewählte Signifikanzniveau, wird die Nullhypothese zurückgewiesen und es wird geschlossen, dass der Datensatz nicht aus einer normalverteilten Grundgesamtheit stammt.
- Andernfalls wird die Nullhypothese nicht zurückgewiesen und es wird geschlossen, dass es keinen statistisch signifikanten Hinweis darauf gibt, dass der Datensatz nicht aus einer normalverteilten Grundgesamtheit stammt.
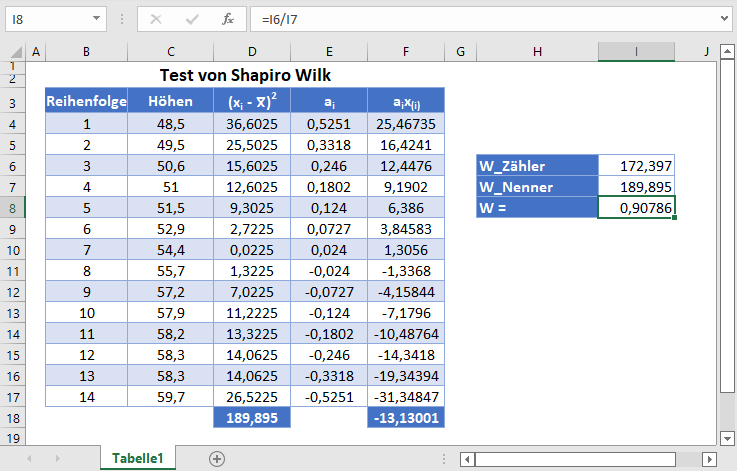
Den Shapiro-Wilk-Test in Excel durchführen
Hintergrund: In der folgenden Tabelle ist eine Stichprobe der Körpergrößen von 14 zehnjährigen Jungen in Zoll dargestellt. Verwenden Sie die Shapiro-Wilk-Methode zum Testen auf Normalität, um zu prüfen, ob die aus der Stichprobe gewonnenen Daten durch eine Normalverteilung modelliert werden können.
Wählen Sie zunächst die Werte im Datensatz aus und sortieren Sie die Daten mit dem Werkzeug Sortieren: Daten > Sortieren (aufsteigend sortieren)

Dadurch werden die Werte folgendermaßen sortiert: 
In neueren Versionen von Excel können Sie alternativ die SORTIEREN-Funktion verwenden, um die Daten zu sortieren:
=SORTIEREN(B2:B15)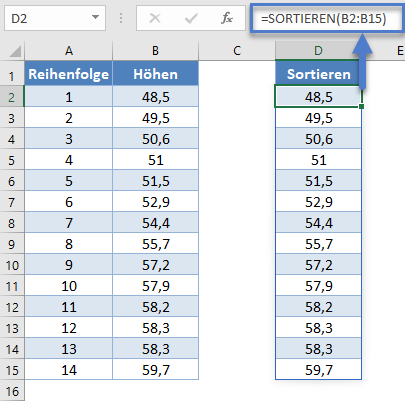
Berechnen Sie als Nächstes den Nenner der W-Statistik
![]()
wie in der folgenden Abbildung gezeigt und verwenden Sie die Funktion MITTELWERT, um den Mittelwert zu berechnen:
=(B2-MITTELWERT($B$2:$B$15))^2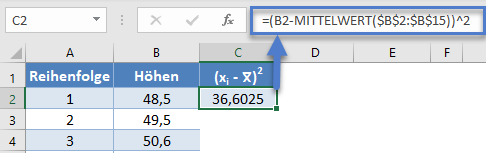
Füllen Sie den Rest der Spalte aus und berechnen Sie dann die Summe (in grünem Hintergrund) wie in der folgenden Abbildung gezeigt:
=SUMME(C2:C15)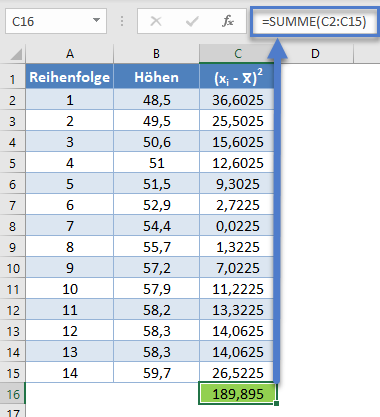
Der Nenner der W-Statistik ist also 189,895.
Als Nächstes werden die Werte von ai, die Koeffizienten der Gewichte des Shapiro-Wilk-Tests für einen Stichprobenumfang von n=14 aus der Shapiro-Wilk-Testtabelle ermittelt. Ein Auszug aus der Tabelle des Shapiro-Wilk-Tests ist unten dargestellt:
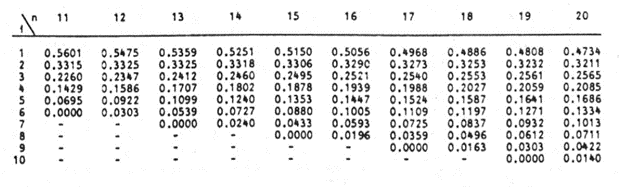
Diese Werte müssen wie folgt manuell eingegeben werden:

Und unter Verwendung der antisymmetrischen Eigenschaft von ai, d. h.an+1-i=-ai für alle i, ergibt sich, dass a14=-a1, a13=-a2, usw. Die vollständigen Werte der Spalte ai sind also in der folgenden Abbildung dargestellt:
=-D8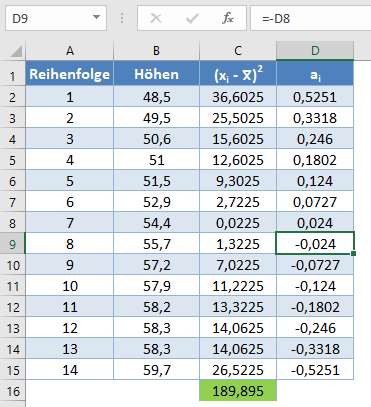
*Beachten Sie, dass es aufgrund der antisymmetrischen Eigenschaft von ai und da der Zähler der W-Statistik ein Quadrat ist, keine Rolle spielt, welche Hälfte der Spalte ai positiv oder negativ ist. Das heißt, Sie können wählen, ob die obere Hälfte der Spalte positiv und die untere Hälfte negativ sein soll oder umgekehrt, ohne dass dies Auswirkungen auf Ihr Endergebnis hat.
Anschließend multiplizieren Sie die ai-Werte mit den entsprechenden (bereits angeordneten) Werten im Datensatz, um die Spalte aix (i) zu erhalten. Die Berechnung und der Wert für den ersten Datenpunkt sind in der folgenden Abbildung dargestellt:
=D2*B2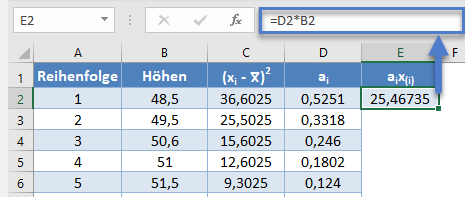
Vervollständigen Sie den Rest der Spalte aix (i) und berechnen Sie die Summe (in grünem Hintergrund) wie in der folgenden Abbildung dargestellt:
=SUMME(E2:E15)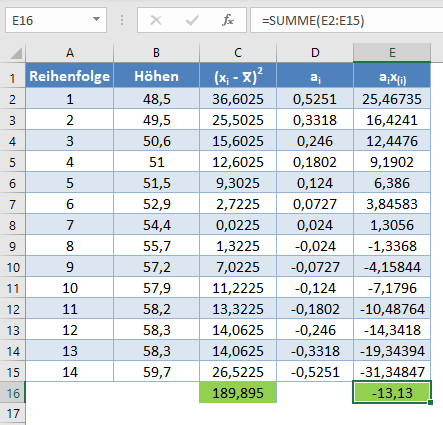
Der Nenner der zuvor ermittelten W-Statistik ist 189,895 , und der Zähler ist das Quadrat der Summe der Spalte aix (i). Daraus ergibt sich Folgendes:
=E16^2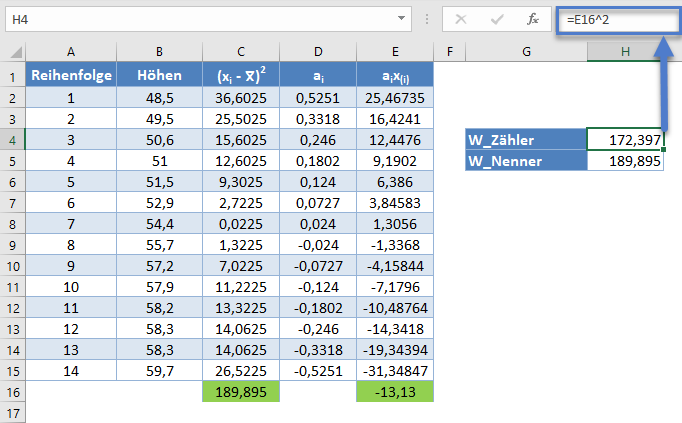
Die W-Statistik ist also wie folgt:
=H4/H5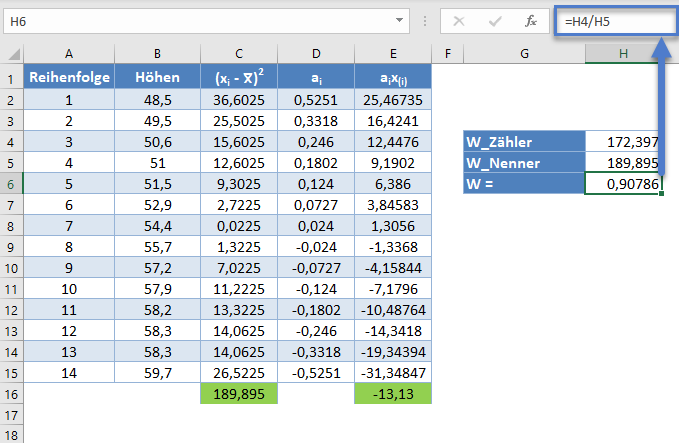
Schließlich wird der p-Wert des Tests mit Hilfe der Shapiro-Wilk-Testtabelle der p-Werte unter Berücksichtigung des Stichprobenumfangs ermittelt.
Ein Auszug aus der Tabelle der p-Werte des Shapiro-Wilk-Tests ist unten dargestellt:
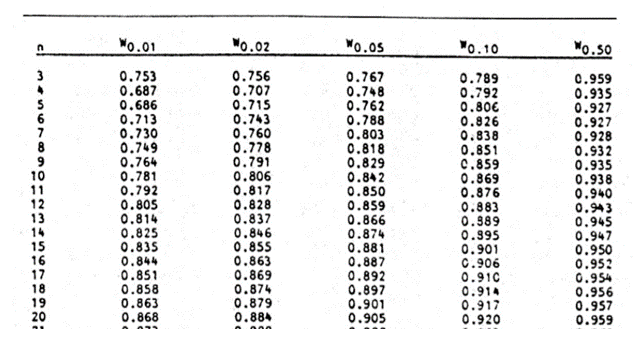
Für diesen Test wird ein Signifikanzniveau (Alpha) von 0,05 verwendet. Aus der Tabelle können Sie ersehen, dass W = 0,90786 zwischen W0,10 = 0,895 und W0,50 = 0,947 für n =14 liegt, was bedeutet, dass der p-Wert zwischen 0,10 und 0,50 liegt. Dies bedeutet, dass der p-Wert größer als α = 0,05 ist, so dass die Nullhypothese nicht verworfen wird.
Daraus schließen wir, dass es nicht genügend Beweise dafür gibt, dass der Datensatz nicht aus einer normalverteilten Grundgesamtheit stammt. Das heißt, wir können davon ausgehen, dass der Datensatz normalverteilt ist.
*Durch lineare Interpolation erhalten Sie einen ungefähren p-Wert von 0,1989.
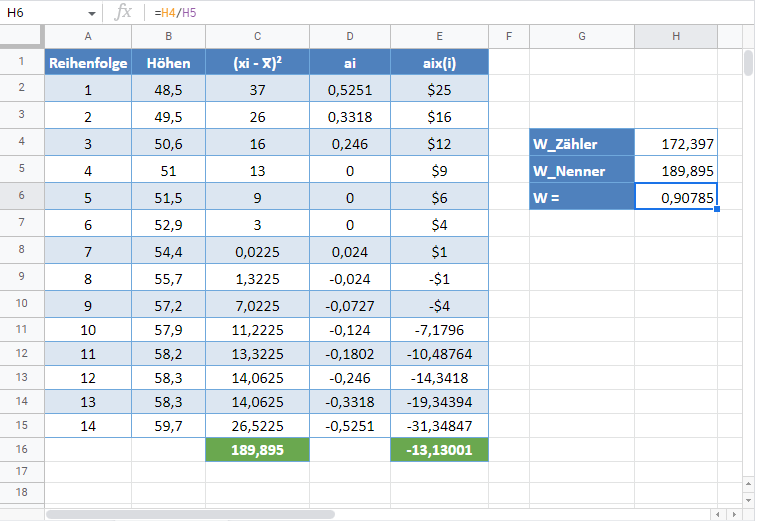
Shapiro-Wilk-Test in Google Sheets
Der Shapiro-Wilk-Test kann in Google Sheets auf ähnliche Weise wie in Excel wie in der folgenden Abbildung gezeigt durchgeführt werden.