In diesem Tutorial zeigen wir Ihnen, wie Sie in Excel und Google Sheets testen können, ob Daten normalverteilt sind (Normalität).

So führen Sie einen Test auf Normalverteilung in Excel durch

Hintergrund: In der folgenden Tabelle ist eine Stichprobe der Körpergrößen (in Zoll) von 30 zehnjährigen Jungen dargestellt. Testen Sie mithilfe der grafischen Methoden des Normalitätstests, ob die aus der Stichprobe gewonnenen Daten durch eine Normalverteilung modelliert werden können.

Die Histogramm-Methode

Ein Histogramm ist eine grafische Darstellung der Häufigkeits- bzw. Wahrscheinlichkeitsverteilung von kontinuierlichen Daten. Die Häufigkeitsverteilung wird durch Rechtecke dargestellt, deren Höhe der Häufigkeit der einzelnen Klassen entspricht und deren Breite die Klassenintervalle bzw. -grenzen darstellt.

Um mit einem Histogramm auf Normalität zu testen, vergleicht man das Histogramm des Datensatzes mit der normalen Wahrscheinlichkeitskurve. Wenn das Histogramm annähernd glockenförmig ist, kann man davon ausgehen, dass der Datensatz normalverteilt ist.

Zunächst wird der Datensatz in Klassen eingeteilt. Sie können die Anzahl der Klassen bestimmen, in die Sie die Daten gruppieren möchten, oder Sie können die Sturges-Regel zur Bestimmung der durch n=1+3,3 logN gegebenen Klassenanzahl in einem Datensatz der Größe N verwenden.

Wenn wir die Sturges-Regel auf unseren Datensatz anwenden, ergibt sich, dass die gewünschte Anzahl von Klassen für unseren Datensatz mit 30 Datenpunkten 6 ist. Dann erhalten wir die Breite jeder Gruppe, indem wir den minimalen Datenpunkt vom maximalen Datenpunkt subtrahieren und das Ergebnis durch die Gruppenanzahl 6 dividieren.

Mit Hilfe der Funktionen Min und Max erhalten wir den minimalen Datenpunkt 48,7 und den maximalen Datenpunkt 59,8.

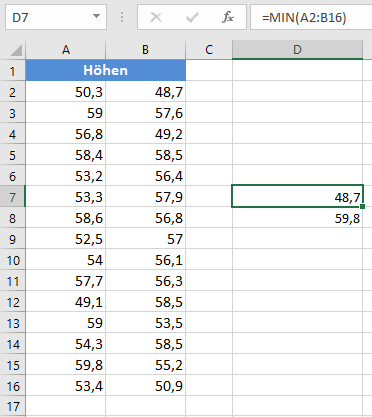
Die Klassenbreite ist also (59,8-48,7)/6=1,85 , aber der Einfachheit halber runden wir die Klassenbreite auf 2 auf und erweitern das Minimum und das Maximum auf 48 bzw. 60. Die Klassenintervalle ergeben sich dann wie folgt:

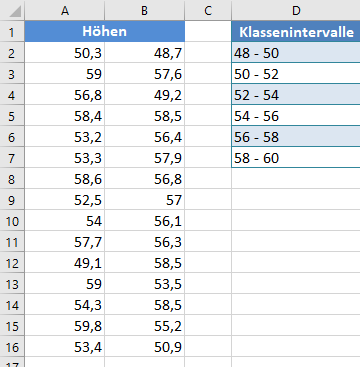
Um ein Histogramm in Excel zu erstellen, benötigen wir die Spalte „Bin“, die die Obergrenzen der Klassenintervalle darstellt. Die Spalte „Bin“ sieht also wie folgt aus:

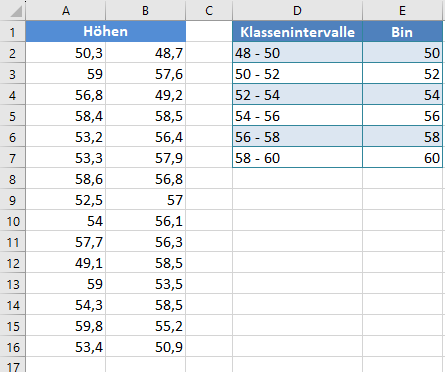
Erstellen Sie nun das Histogramm der Daten.

Verwenden Sie die Funktion „Histogramm“ in der Menüleiste Daten > Datenanalyse.

Wenn Sie die Option „Datenanalyse“ nicht sehen, müssen Sie das Datenanalyse-Toolpak installieren.

Wählen Sie im Fenster Datenanalyse die Option Histogramm und klicken Sie auf OK.

Konfigurieren Sie die Parameter wie folgt.

• Klicken Sie auf „Eingabebereich“ und wählen Sie die Zellen aus, die die Quelldaten enthalten.
• Klicken Sie auf „Klassenbereich“ und wählen Sie die Zellen aus, die die Intervalle (Bins) enthalten.
• Aktivieren Sie das Kontrollkästchen „Beschriftungen“, wenn der ausgewählte Bereich Spaltenüberschriften enthält. In diesem Fall haben wir die Überschriften nicht einbezogen und daher das Kontrollkästchen „Beschriftungen“ nicht aktiviert.
• Wählen Sie die gewünschte Ausgabeoption. Um die Ergebnisse auf demselben Blatt zu erhalten, wählen Sie den Ausgabebereich und geben Sie den spezifischen Verweis auf die Zelle an, in der die Matrix angezeigt werden soll. In unserem Fall ist es $G$1
• Um ein effektives Ergebnis bei der Bestimmung der Verteilungsform mit Hilfe des Histogramms zu erzielen, sollten Sie die Kontrollkästchen „Pareto (sortiertes Histogramm)“ und „Kumulierte Häufigkeit“ nicht aktivieren.
• Aktivieren Sie schließlich das Kontrollkästchen „Diagrammdarstellung“, um das Histogramm anzuzeigen.

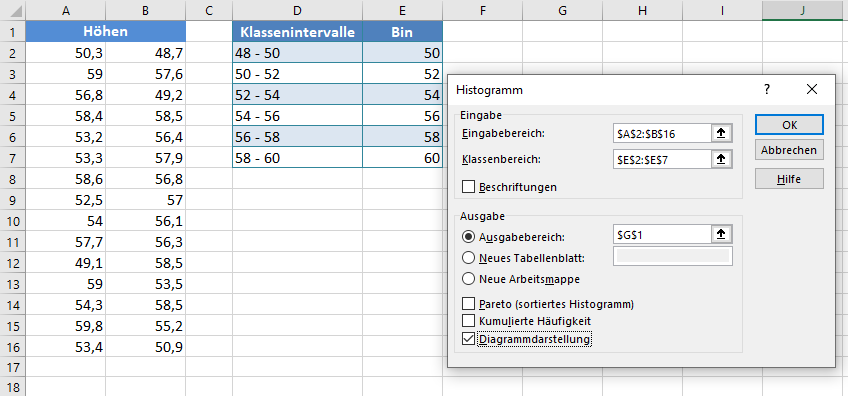
Die Ausgabe des Histogramms sieht wie folgt aus:

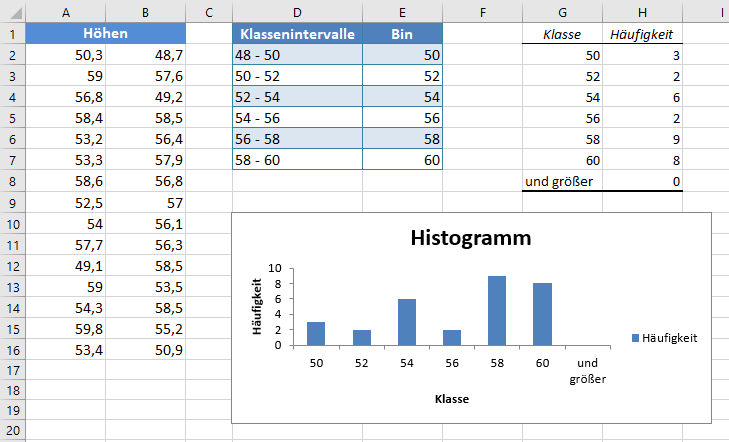
Damit das Diagramm mehr wie ein Histogramm aussieht, nehmen wir einige Anpassungen wie folgt vor:

• Löschen Sie zunächst die Zeile „und Größer“ aus der Tabelle „Klasse/Häufigkeit“.
• Klicken Sie dann mit der rechten Maustaste auf eines der Rechtecke und wählen Sie die Option „Datenreihe formatieren…“.

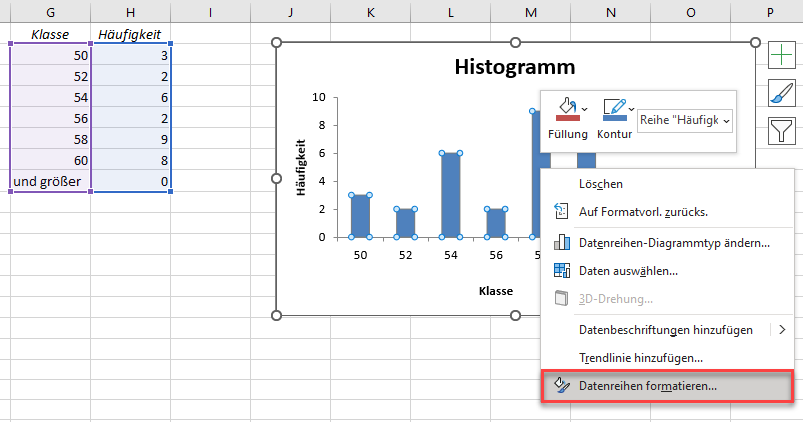
• Bewegen Sie bei der Option „Datenreihenoptionen“ den Schieberegler im Abschnitt „Abstandsbreite“ auf die Seite „Kein Lücke“ oder geben Sie „0%“ in das Feld im Abschnitt „Abstandsbreite“ ein.

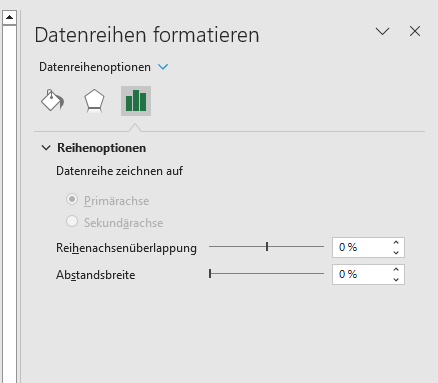
Die endgültige Ausgabe des Histogramms sieht dann wie folgt aus:

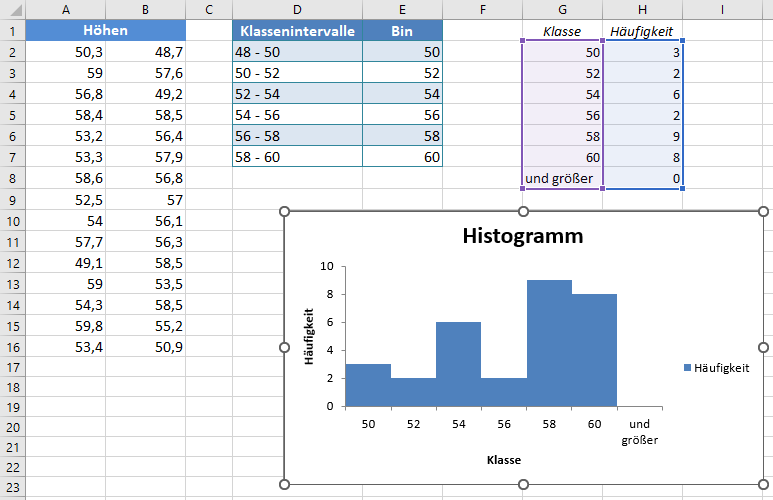
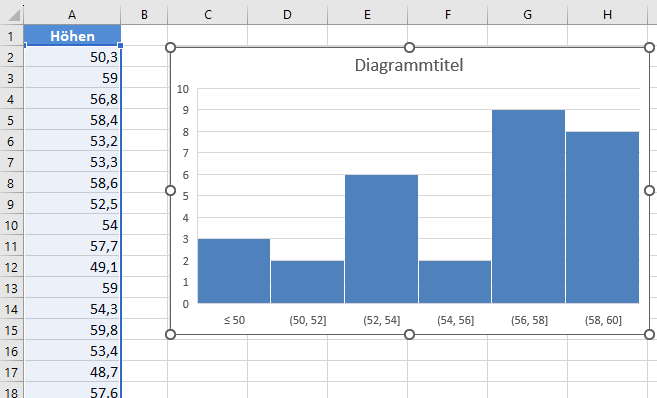
Es ist deutlich zu erkennen, dass das Histogramm weder glockenförmig noch symmetrisch um den Mittelpunkt ist. Daraus können wir schließen, dass die gegebenen Daten durch eine Normalverteilung nicht modelliert werden können.

Wenn Sie Excel 2016, eine neuere Version oder die Microsoft 365-Pakete verwenden, können Sie ein Histogramm alternativ über Einfügen > Statistikdiagramm einfügen > Histogramm erstellen.

Platzieren Sie den Datensatz in einer Spalte, wählen Sie die Daten zusammen mit der Beschriftung aus und klicken Sie dann auf Einfügen > Statistikdiagramm einfügen > Histogramm. In unserem Fall haben wir die folgende Ausgabe:

Passen Sie nun das Diagramm an Ihre Wünsche an, indem Sie die Anzahl der Klassen und die Klassenbreite konfigurieren. Klicken Sie mit der rechten Maustaste auf die horizontale Achse und klicken Sie auf Achse formatieren:

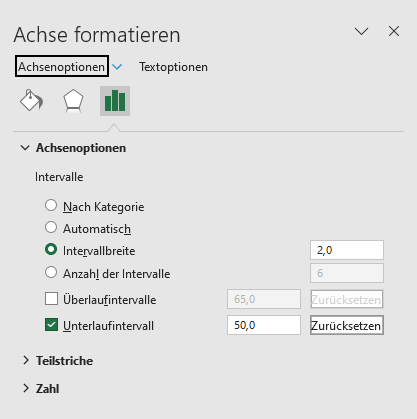
Legen Sie unter Achsenoptionen die Intervallbreite oder die Anzahl der Intervalle fest, legen Sie das Überlaufintervall und/oder das Unterlaufintervall fest. Das Überlaufintervall ist ein Punkt im Datensatz, bei dem alle Werte, die größer als er sind, in einer Klasse gruppiert werden, während das Unterlaufintervall ein Punkt ist, bei dem alle Werte, die kleiner als er sind, in einer Klasse gruppiert werden.

In unserem Fall haben wir die Intervallbreite auf 2 und das Unterlaufintervall auf 50 gesetzt (siehe unten):

Das angepasste Diagramm ist unten dargestellt:

Boxplot-Methode

Ein Boxplot ist ein Diagramm, das die fünfstellige Zusammenfassung eines Datensatzes darstellt. Es zeigt den Mindest- und den Höchstwert, das erste und das dritte Quartil sowie den Median. Der Median wird durch eine Linie, die ein Rechteck in zwei Teile unterteilt, dargestellt. Die parallelen Kanten des Rechtecks stellen das erste und das dritte Quartil dar. Von den Quartilen werden senkrechte Linien (die so genannten Whisker) zu den Minimal- und Maximalwerten gezogen.

Bei normalverteilten Daten befindet sich die Medianlinie des Boxplot-Diagramms ungefähr in der Mitte des Rechtecks, während die beiden Whisker ungefähr gleich lang sind. Bei einem Datensatz, der die oben genannten Bedingungen erfüllt, kann also davon ausgegangen werden, dass er normalverteilt ist, andernfalls sind die Daten nicht normalverteilt.

In Excel-Versionen vor 2016 ist das Boxplot-Diagramm nicht in den Diagrammvorlagen enthalten. Es gibt jedoch eine alternative Lösung, die ich Ihnen in diesem Artikel vorstellen werde. Ich zeige Ihnen auch, wie Sie das Boxplot-Diagramm mithilfe der Boxplot-Diagrammvorlage in Excel 2016 und späteren Versionen erstellen können.

In den folgenden Schritten zeige ich Ihnen, wie Sie das Boxplot-Diagramm in Excel-Versionen vor 2016 anhand des obigen Beispiels der Körpergrößen von Jungen erstellen können.

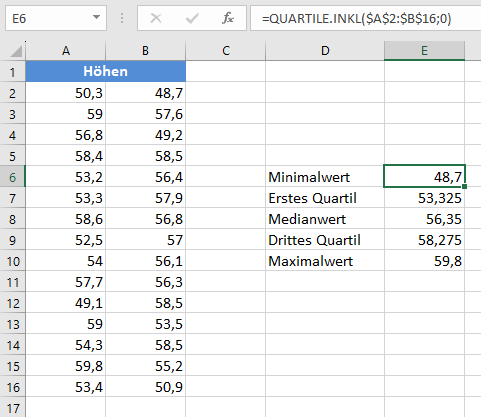
Berechnen Sie zunächst wie, unten gezeigt, die Quartil-Werte aus dem Datensatz mithilfe der Funktion QUARTILE.INKL mit den Parameterwerten: 0 für den Mindestwert, 1 für das erste Quartil, 2 für den Median, 3 für das dritte Quartil und 4 für den Maximalwert:

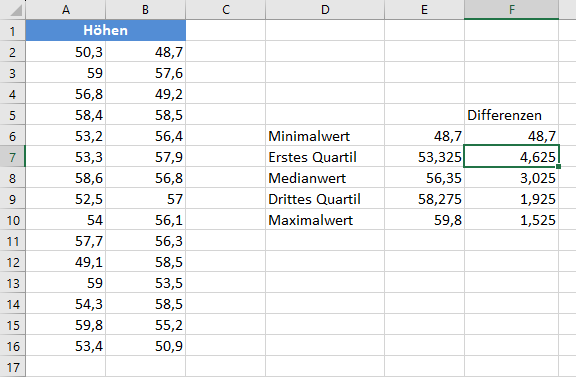
Berechnen Sie dann die Differenzen zwischen jedem Quartilswert und seinem vorhergehenden, wobei der Mindestwert konstant bleibt. Erstellen Sie also eine Spalte mit der Bezeichnung „Differenzen“, die, wie unten dargestellt, in der ersten Zeile den Mindestwert, in der zweiten Zeile den Mindestwert des ersten Quartils, in der dritten, vierten und fünften Zeile den Medianwert des ersten Quartils, den Medianwert des dritten Quartils und den Maximalwert des dritten Quartils enthält:

Als Nächstes erstellen Sie ein gestapeltes Säulendiagramm über Einfügen > Säulen- und Balkendiagramm einfügen > Gestapelte Säulen unter Verwendung der Spalte „Differenzen“.

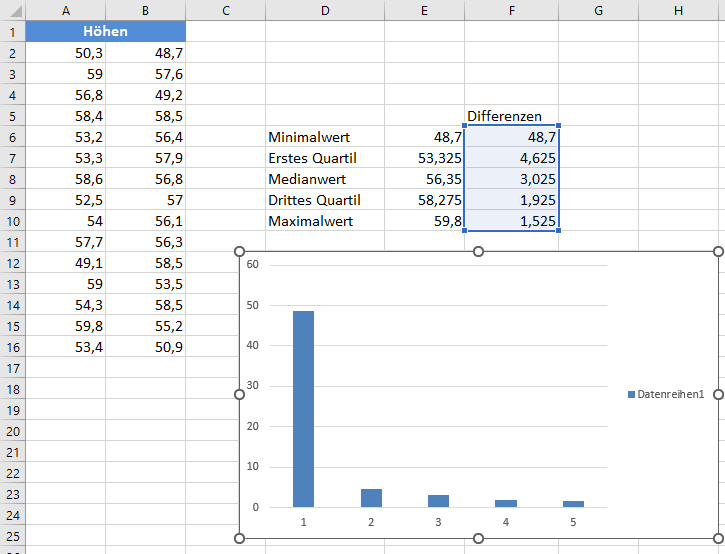
Anschließend kehren Sie die Achsen des Diagramms um, indem Sie mit der rechten Maustaste auf das Diagramm klicken und auf Daten auswählen > Zeile/Spalte tauschen und dann auf OK klicken.

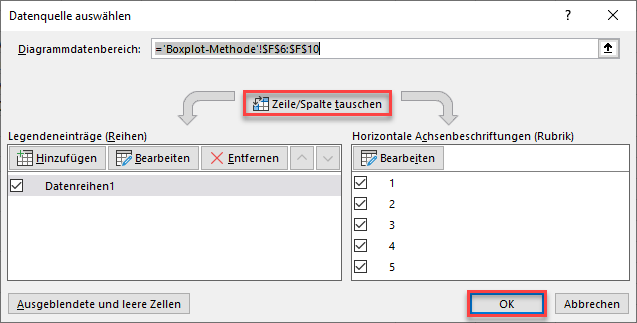
Das Diagramm ändert sich dann in:

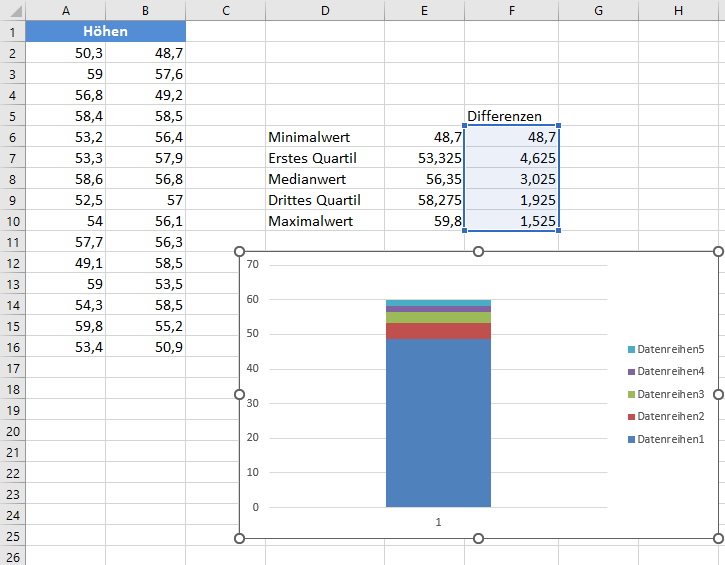
Konvertieren Sie anschließend das Diagramm in einen Boxplot, indem Sie die folgenden Schritte ausführen:

• Blenden Sie die untere Datenreihe aus, indem Sie mit der rechten Maustaste auf den unteren Teil des Säulendiagramms klicken und auf Datenreihe formatieren… klicken , auf der Registerkarte Füllung die Option Keine Füllung wählen und dann das Popup-Fenster schließen.

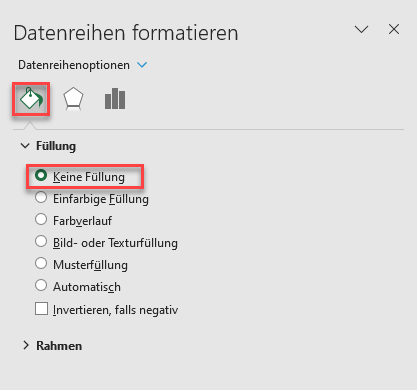
Das Diagramm wird nun angezeigt:

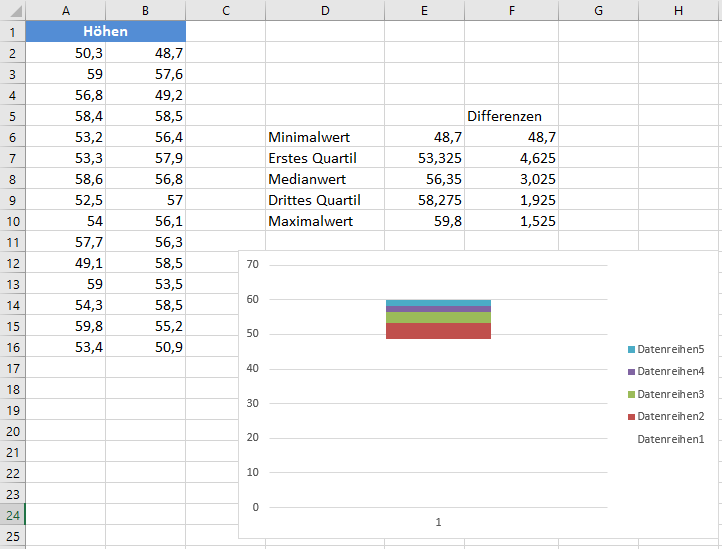
• Erstellen Sie Die Whisker für den Boxplot-Diagramm, indem Sie den obersten und den unteren farbigen Teil des Säulendiagramms durch Linien (oder Whiskers) ersetzen. Klicken Sie mit der rechten Maustaste auf den obersten Teil des Säulendiagramms und klicken Sie auf Datenreihe formatieren…, wählen Sie auf der Registerkarte Füllung die Option Keine Füllung und schließen Sie das Popup-Fenster. Klicken Sie dann in der Multifunktionsleiste auf Diagrammentwurf > Diagrammelement hinzufügen > Fehlerbalken > Standardabweichung, oder klicken Sie im Abschnitt Diagrammwerkzeuge in der Menüleiste auf Layout > Fehlerbalken > Fehlerbalken mit Standardabweichung.

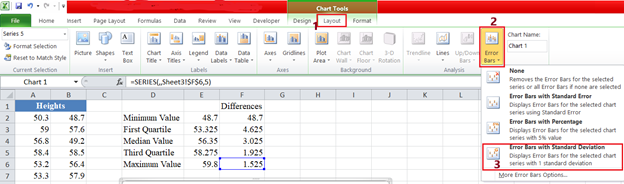
Wählen Sie auch unter Layout > Fehlerbalken die Option Weitere Fehlerbalkenoptionen. Legen Sie in der Option Vertikale Fehlerbalken die Richtung auf Minus, das Endtyp auf Keine Kappe und den Fehlerbetrag auf 100 fest.

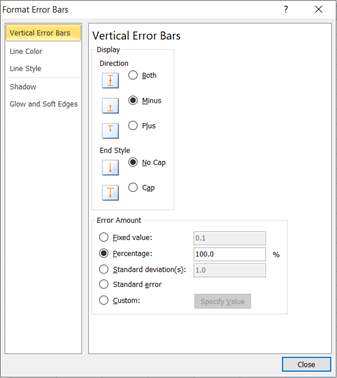
Wiederholen Sie die obigen Schritte für die zweite Datenreihe von unten (der jetzt untere farbige Teil).

Das Diagramm sieht dann wie folgt aus:

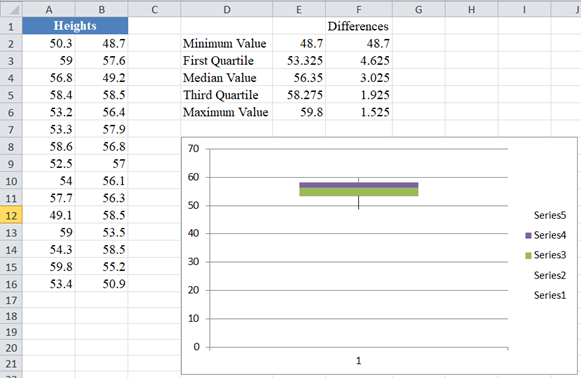
• Schließlich formatieren wir den mittleren Bereich wie folgt: Klicken Sie mit der rechten Maustaste auf den oberen farbigen Teil des Boxplot-Diagramms und klicken Sie auf Datenreihe formatieren…, wählen Sie auf der Registerkarte Füllung die Option Keine Füllung und auf der Registerkarte Rahmenfarbe die Option Durchgezogene Linie, setzen Sie dann die Farbe auf Schwarz und schließen Sie das Popup-Fenster.

Wiederholen Sie den obigen Schritt für den letzten farbigen Teil. Sie können auch die Achsen formatieren, indem Sie die Bereiche so anpassen, dass das Boxplot-Diagramm größer und besser aussieht. Das Diagramm sieht nun wie folgt aus:

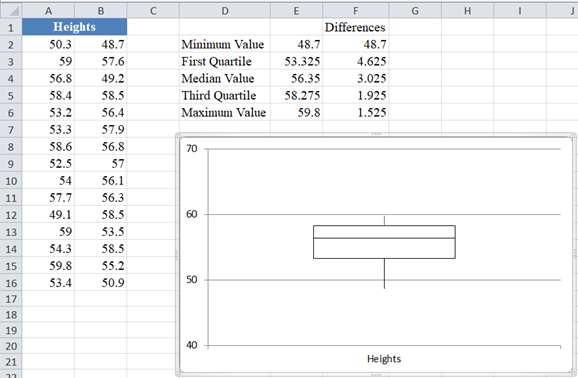
Aus dem Boxplot-Diagramm ist ersichtlich, dass die Linie das Rechteck in zwei Teile geteilt hat, so dass der untere Teil des Rechtecks größer als der obere Teil ist. Außerdem ist der untere Whisker länger als der obere. Daraus lässt sich schließen, dass der Datensatz keine normalverteilten Daten darstellt.

Wenn Sie Excel 2016, eine neuere Version oder die Microsoft 365-Pakete verwenden, können Sie alternativ ein Boxplot-Diagramm erstellen, indem Sie den Datensatz auswählen und auf Einfügen > Statistikdiagramm einfügen > Kastengrafik klicken.

Die Ausgabe wird unten angezeigt:

Sie können dann die Achsen formatieren, um den Boxplot nach Ihren Wünschen größer und übersichtlicher zu gestalten.

Die P-P-Plot-Methode

Ein P-P-Plot (kurz für Probability – Probability Plot oder Percent – Percent Plot) ist ein Diagramm, das verwendet wird, um festzustellen, ob ein bestimmter Datensatz einer bestimmten Wahrscheinlichkeitsverteilung entspricht. Um die Normalität mit Hilfe eines P-P-Diagramms zu prüfen, werden die kumulativen Wahrscheinlichkeiten der Ränge der Datensatzwerte gegen die entsprechenden Wahrscheinlichkeiten der durch die Normalverteilung prognostizierten Werte dargestellt. Wenn die resultierende Grafik annähernd eine Gerade ist, kann davon ausgegangen werden, dass der Datensatz normalverteilt ist, andernfalls ist der Datensatz nicht normalverteilt.

In den folgenden Schritten zeigen wir Ihnen, wie Sie ein P-P-Diagramm der Normalwahrscheinlichkeit anhand des obigen Beispiels der Körpergrößen von Jungen erstellen können.

Legen Sie zunächst den Datensatz in eine Spalte, wählen Sie die Werte im Datensatz aus und sortieren Sie die Daten: Daten > Nach Größe sortieren (aufsteigend), um die Werte, wie unten gezeigt, in aufsteigender Reihenfolge anzuordnen:

Die sortierten Werte sehen wie folgt aus:

Verwenden Sie anschließend die Funktion RANG.GLEICH, um die Ränge der Datensatzwerte wie folgt zu ermitteln.

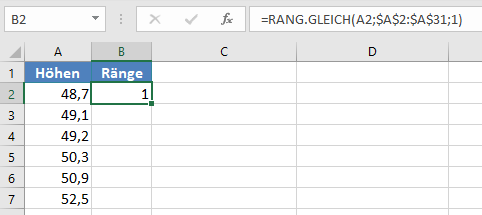
Vervollständigen Sie die Ränge der restlichen Datensatzwerte.

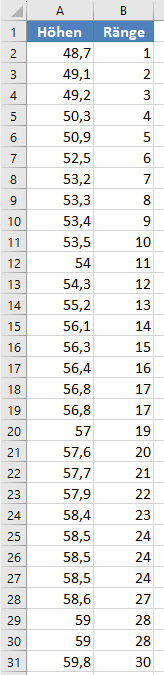
Die Funktion RANG.GLEICH gibt den obersten Rang einer Wertegruppe zurück, die denselben Rang hat. Für die Zwecke dieser Darstellung benötigen wir jedoch stattdessen die unteren Ränge. Daher werden wir die Ränge der Werte, die denselben Rang haben, manuell ändern. Wir ändern also die folgenden Ränge:

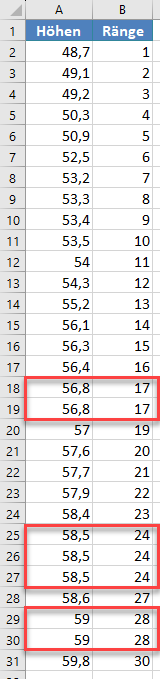
zu:

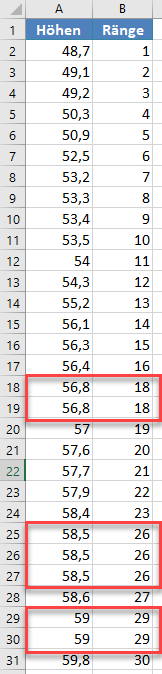
Berechnen Sie nun die kumulativen Wahrscheinlichkeiten der Datensatzränge. Wir werden diese Formel verwenden:

wobei i für den Rang und n für die Größe des Datensatzes (Anzahl der Werte) steht. Wir haben also:

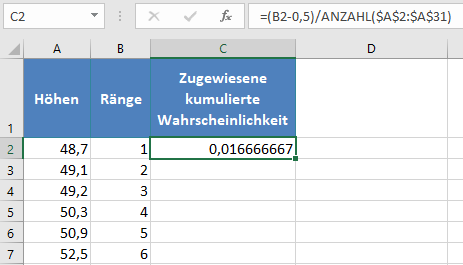
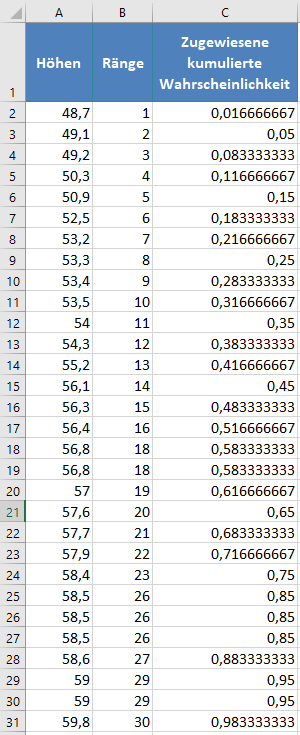
Vervollständigen Sie den Rest der zugewiesenen kumulativen Wahrscheinlichkeiten wie unten dargestellt:

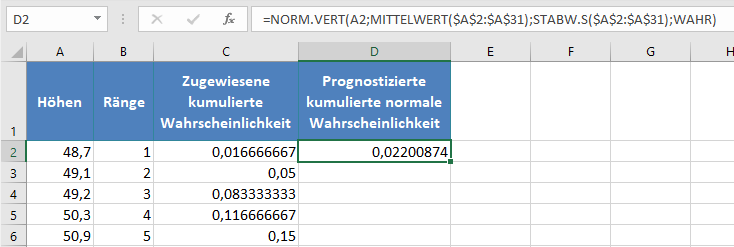
Berechnen Sie als Nächstes die prognostizierte kumulative Normalwahrscheinlichkeit für den Datensatz mithilfe der Funktion NORM.VERT. x ist der Wert aus dem Datensatz, Mittelwert ist der Durchschnitt des Datensatzes und Standabwn ist die Standardabweichung des Datensatzes und kumuliert ist WAHR. Somit haben wir:

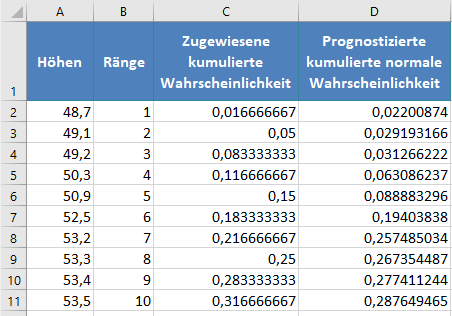
Vervollständigen Sie den Rest der prognostizierten kumulierten Normalwahrscheinlichkeiten wie unten gezeigt:

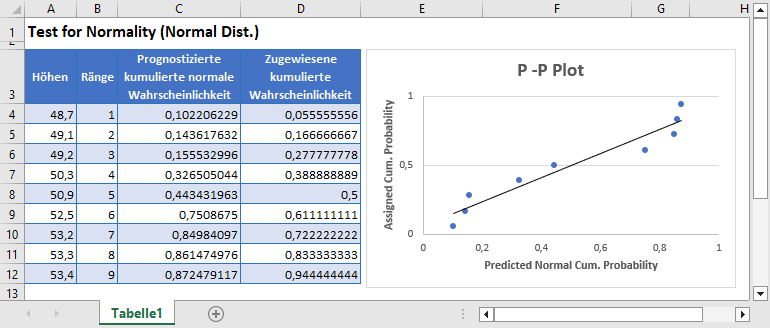
Zeichnen Sie schließlich ein Streudiagramm mit der prognostizierten kumulierten Normalwahrscheinlichkeit auf der x-Achse und der zugewiesenen kumulierten Wahrscheinlichkeit auf der y-Achse. Ich muss die Positionen der prognostizierten kumulierten Normalwahrscheinlichkeit und der zugewiesenen kumulierten Wahrscheinlichkeit vertauschen, so dass die prognostizierte kumulierte Normalwahrscheinlichkeit an erster Stelle steht. Wählen Sie die beiden Spalten mit den Beschriftungen aus und klicken Sie, wie unten gezeigt, auf Einfügen > Punkt(X,Y) oder Blasendiagramm einfügen  > Punkt(X,Y):

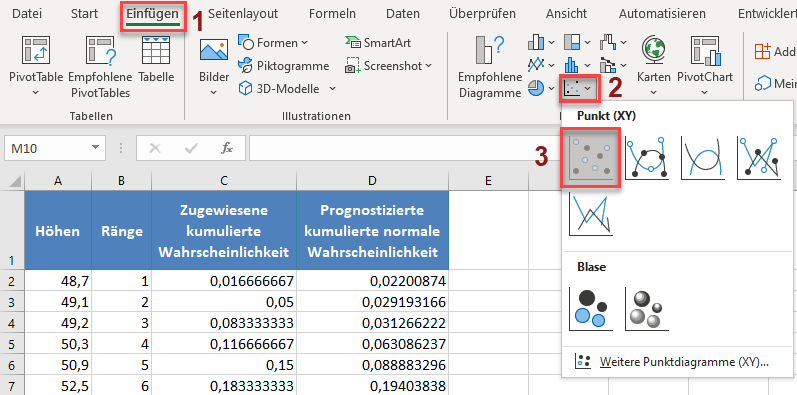
Wir erhalten das folgende Diagramm:

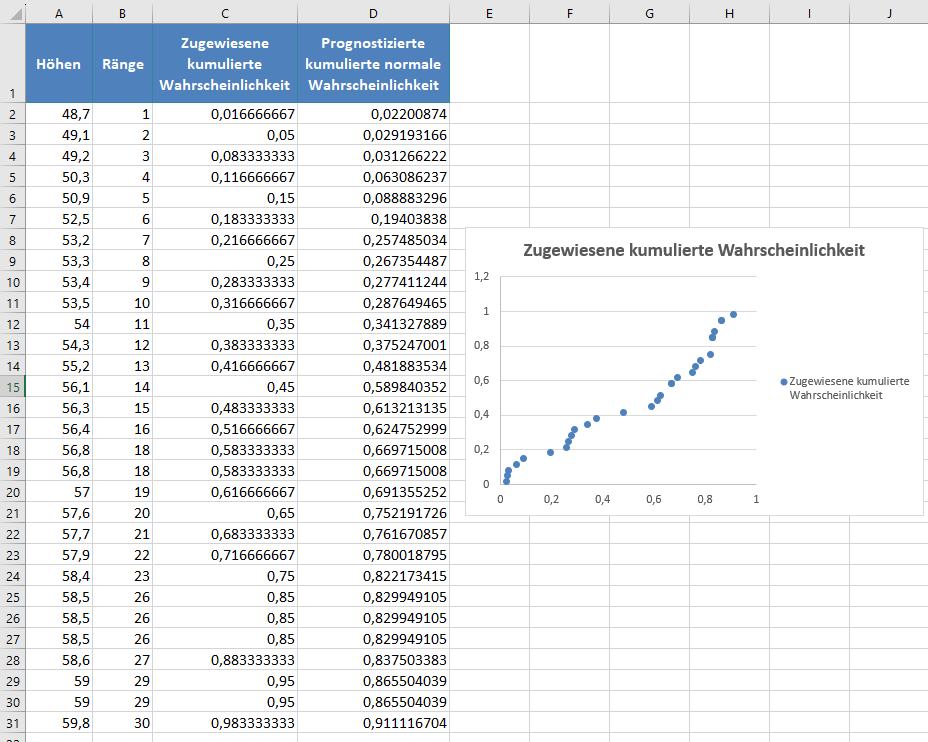
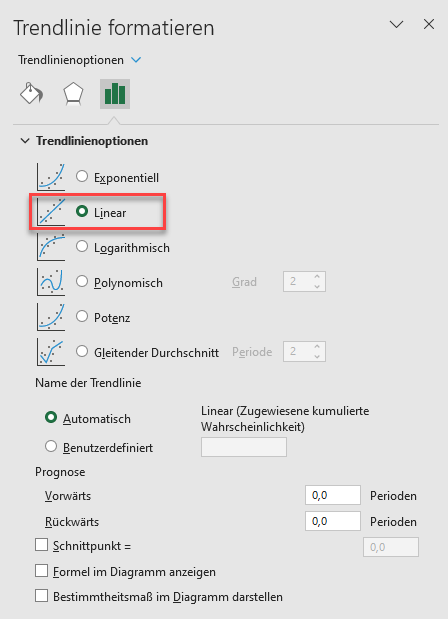
Fügen Sie dann die Trendlinie zum Diagramm hinzu, indem Sie mit der rechten Maustaste auf einen der Datenpunkte im Diagramm klicken und Trendlinie hinzufügen wählen. Vergewissern Sie sich in den Trendlinienoptionen, dass der Trend-/Regressionstyp auf Linear eingestellt ist, und schließen Sie dann das Fenster.

Sie können auch einige andere Anpassungen am Diagramm vornehmen, z. B. die Achsentitel hinzufügen und den Titel bearbeiten. Das Ergebnis sieht dann wie unten dargestellt aus:

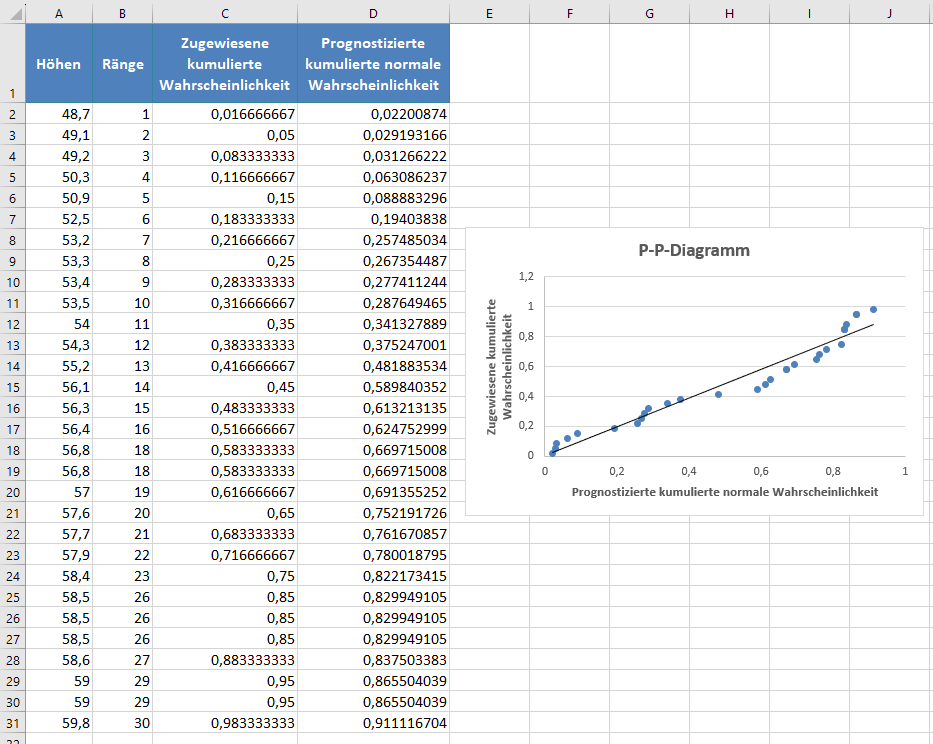
Aus dem P-P-Diagramm können wir ersehen, dass viele der Datenpunkte deutlich von der Trendlinie abweichen, woraus wir schließen können, dass die Daten nicht normal verteilt sind.

Das Q-Q-Diagramm verwenden

Ein Q-Q-Diagramm (kurz für Quantil-Quantil-Diagramm) ist ein Diagramm, das verwendet wird, um festzustellen, ob ein bestimmter Datensatz einer bestimmten Wahrscheinlichkeitsverteilung entspricht. Das Q-Q-Diagramm ähnelt der P-P-Darstellung, mit dem Unterschied, dass die Quantile des Datensatzes bei der Q-Q-Darstellung gegen ihre entsprechende, durch die Normalverteilung prognostizierte Quantile dargestellt werden. Wenn die resultierende Grafik annähernd eine gerade Linie ist, kann davon ausgegangen werden, dass der Datensatz normalverteilt ist, andernfalls ist der Datensatz nicht normalverteilt.

In den folgenden Schritten zeige ich Ihnen, wie Sie ein Q-Q-Diagramm der Normalwahrscheinlichkeit anhand des obigen Beispiels der Körpergrößen von Jungen erstellen können.

Führen Sie zunächst die im Abschnitt „P-P-Diagramm“ beschriebenen Schritte aus, um die zugewiesenen kumulativen Wahrscheinlichkeiten des Datensatzes zu erhalten (siehe unten):

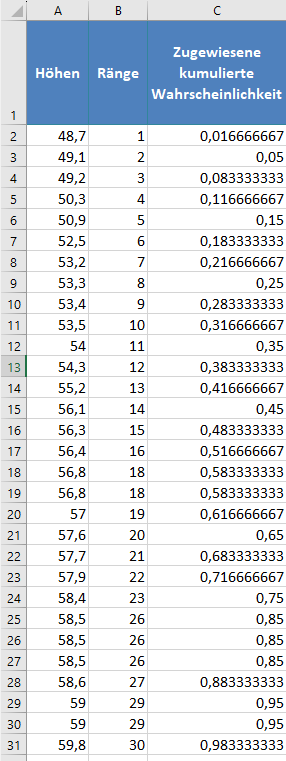
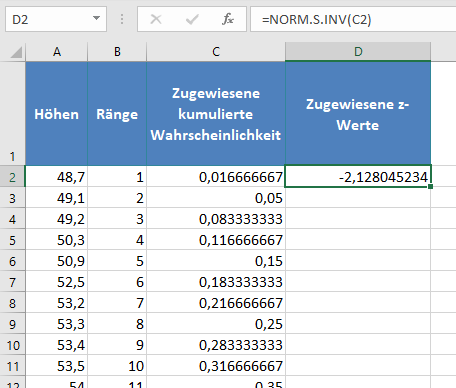
Berechnen Sie anschließend den z-Wert, der jeder der zugewiesenen kumulierten Wahrscheinlichkeiten entspricht, indem Sie die Funktion NORM.S.INV verwenden, wobei Wahrsch der Wert der zugewiesenen kumulierten Wahrscheinlichkeit ist. Somit haben wir:

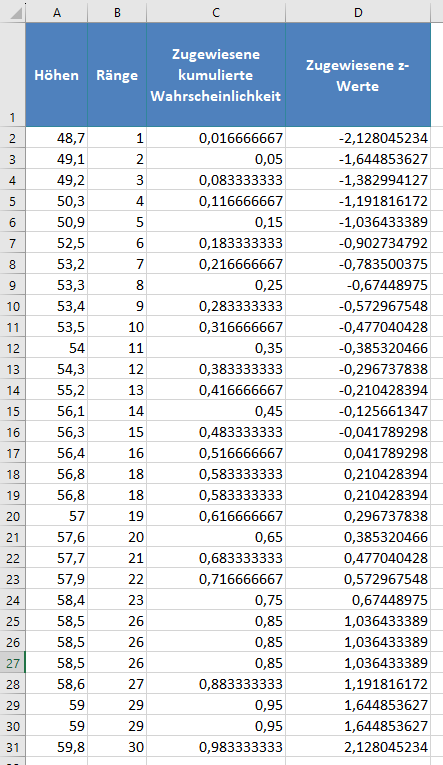
Füllen Sie den Rest der Spalte mit den zugewiesenen z-Werte wie unten gezeigt aus:

Berechnen Sie als nächstes die normalen prognostizierten z-Werte für den Datensatz mit der folgenden Formel

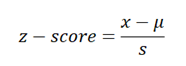
wobei x der Wert aus dem Datensatzes, μ der Mittelwert und s die Standardabweichung des Datensatzes ist. Wir haben also:

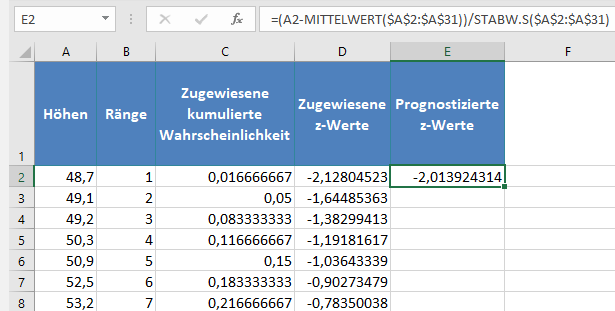
Vervollständigen Sie den Rest der prognostizierten z-Werte wie unten gezeigt:

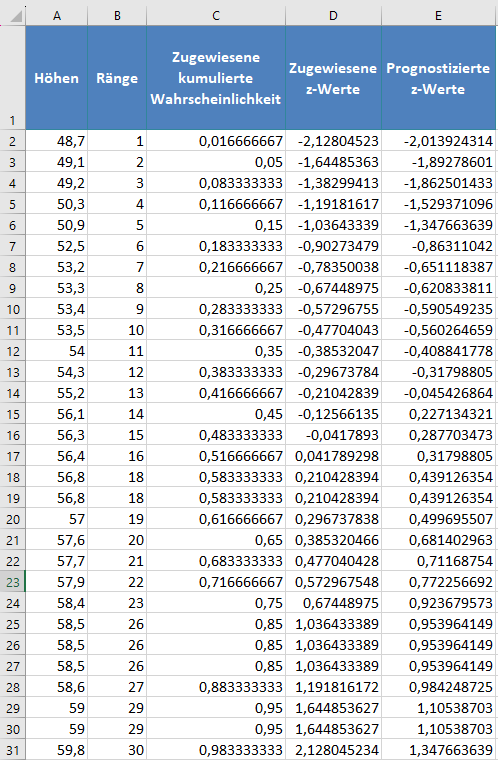
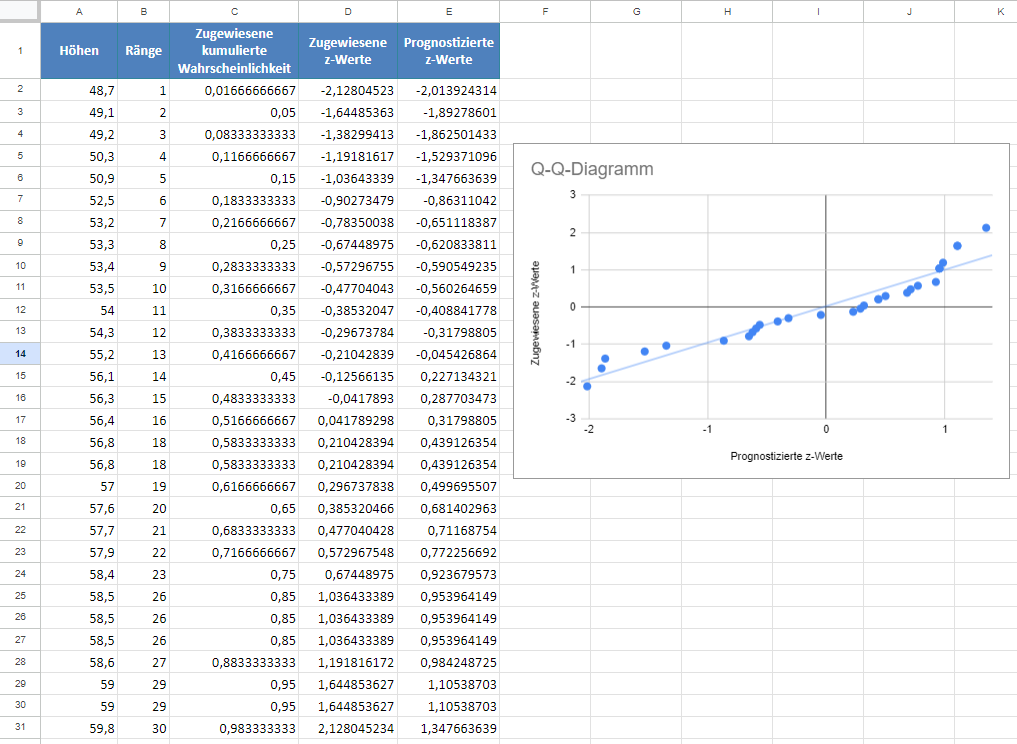
Vertauschen Sie schließlich die Positionen der Spalten „Prognostizierte z-Werte“ und „Zugewiesene z-Werte“ und erstellen Sie, wie unten dargestellt, ein Streudiagramm nach dem im Abschnitt „P-P-Diagramm“ beschriebenen Verfahren mit der Spalte „Prognostizierte z-Werte“ auf der x-Achse und „Zugewiesene z-Werte“ auf der y-Achse:

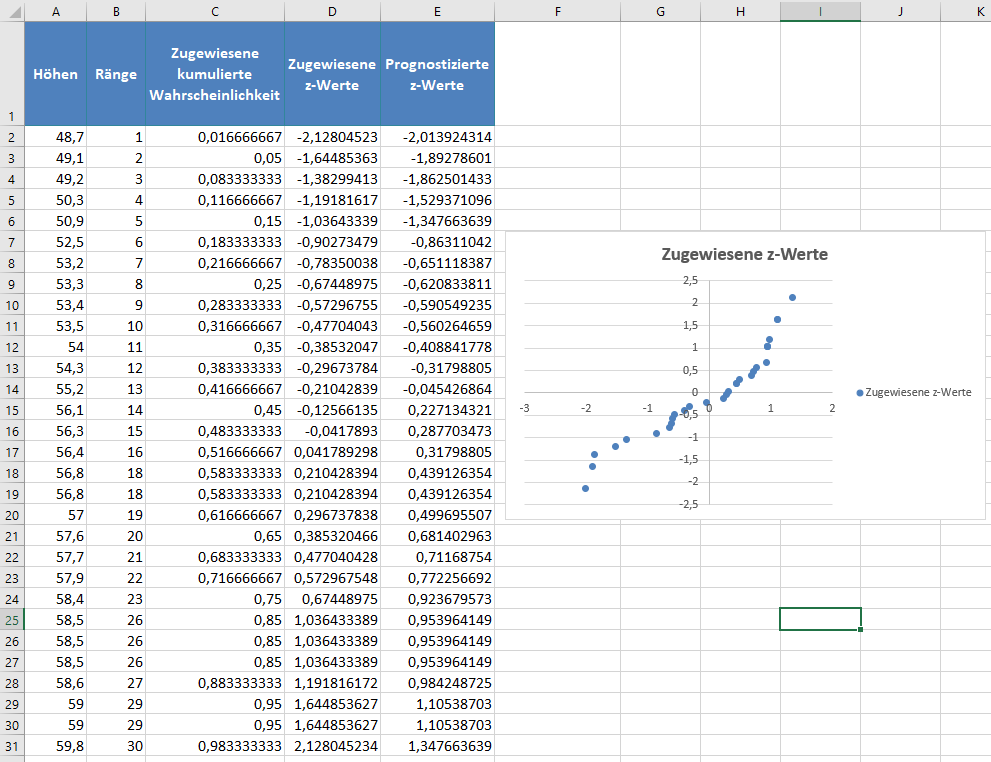
Fügen Sie dann, wie im Abschnitt „P-P-Diagramm“ beschrieben, die Trendlinie zum Diagramm hinzu (siehe unten):

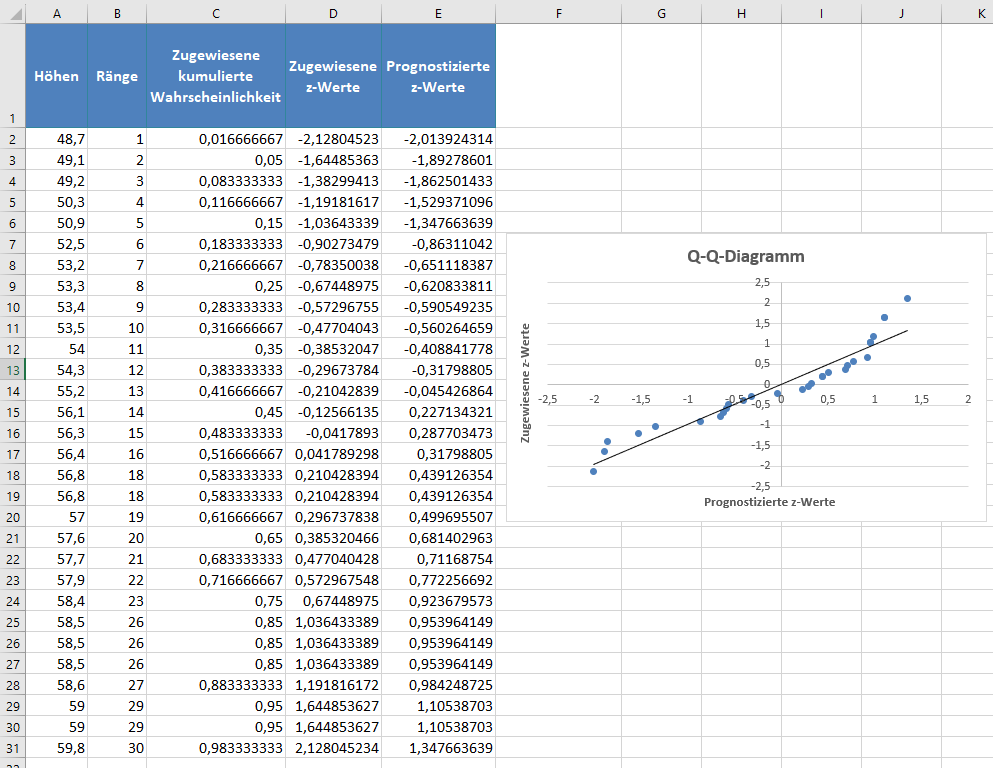
Aus dem Q-Q-Diagramm können wir ersehen, dass viele Datenpunkte deutlich von der Trendlinie abweichen, woraus wir schließen können, dass die Daten nicht normal verteilt sind.

Test auf Normalverteilung in Google Sheets

Der Test auf Normalverteilung kann in Google Sheets auf ähnliche Weise wie in Excel durchgeführt werden.

Histogramm in Google Sheets

Um ein Histogramm in Google Sheets zu erstellen, markieren Sie den Datensatz und klicken Sie, wie unten gezeigt, auf Einfügen > Diagramm:

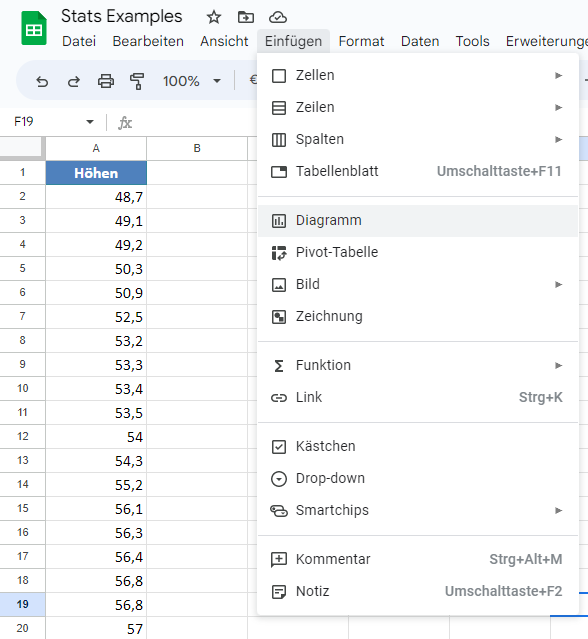
Stellen Sie im Diagrammeditor auf der Registerkarte Einrichtung unter Sonstiges den Diagrammtyp auf Histogramm ein, aktivieren Sie das Kontrollkästchen Zeile 1 für Kopfzeile verwenden, wenn der Titel in Ihrem markierten Datenbereich enthalten ist, und nehmen Sie gegebenenfalls weitere Anpassungen vor. Dies ist in der folgenden Abbildung dargestellt:

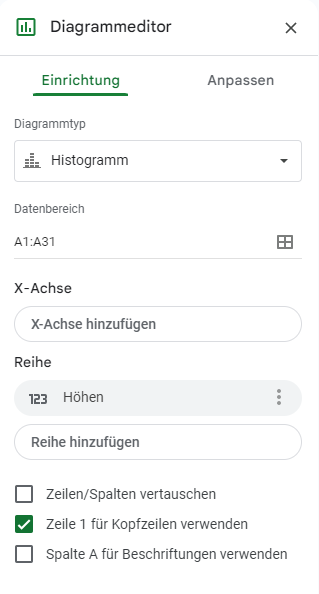
Stellen Sie auf der Registerkarte Anpassen unter der Option Histogramm die Klassengröße auf die gewünschte Intervallbreite des Datensatzes ein. In unserem Fall beträgt die Intervallbreite 2, wie in der Abbildung unten gezeigt:

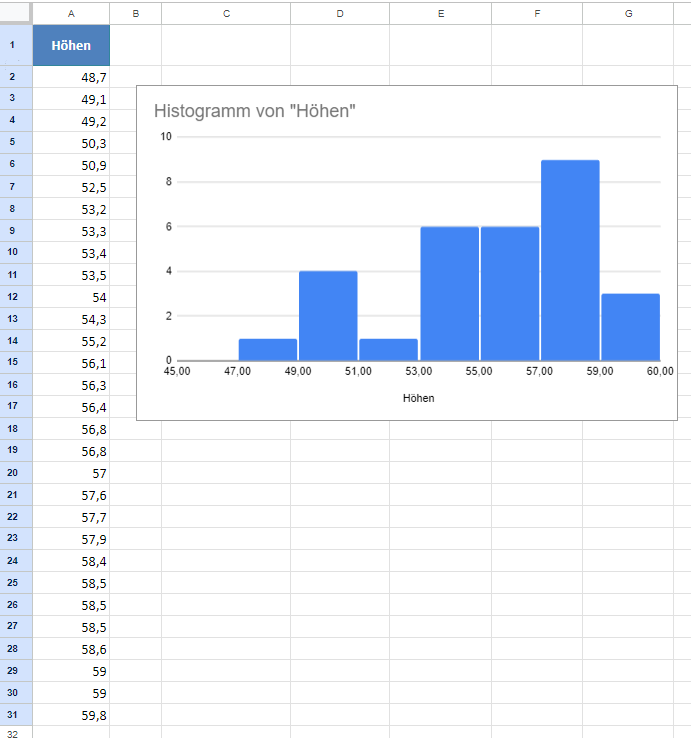
Und wir erhalten die folgende Ausgabe:

Boxplot-Diagramm in Google Sheets

Google Sheets hat keine Boxplot-Vorlage in seinen Diagrammvorlagen. Sie können jedoch das Kerzendiagramm verwenden, um ein ähnliches Diagramm wie ein Boxplot zu erstellen, mit der Ausnahme, dass der Medianwert in einem Kerzendiagramm nicht enthalten ist. Daher können Sie mit einem Kerzendiagramm möglicherweise keine angemessenen Schlussfolgerungen hinsichtlich der Normalverteilung eines Datensatzes ziehen.

Das P-P- und Q-Q-Diagramm in Google Sheets

Die P-P- und Q-Q-Diagramme können in Google Sheets auf ähnliche Weise wie in Excel erstellt werden. Um P-P- und Q-Q-Diagramme in Google Sheets zu erstellen, verwenden Sie dieselben Methoden wie in den Abschnitten P-P-Diagramm und Q-Q-Diagramm für Excel, um die Achse zu erhalten, die für die Erstellung des Diagramms verwendet werden soll.

Markieren Sie anschließend die Spalten „Prognostizierte kumulierte Normalwahrscheinlichkeit“ und „Zugewiesene kumulierte Wahrscheinlichkeit“ für das P-P-Diagramm oder die Spalten „Prognostizierter z-Wert“ und „Zugewiesener z-Wert“ für das Q-Q-Diagramm und klicken Sie auf Einfügen > Diagramm.

Stellen Sie im Diagrammeditor auf der Registerkarte Einrichtung den Diagrammtyp auf Streudiagramm ein. Google Sheets stellt die beiden Spalten in der Regel als zwei unabhängige Diagramme dar. Um dies zu ändern, wählen Sie die richtige Spalte für die x-Achse in der Option X-Achse aus und entfernen Sie die Spalte für die x-Achse aus den Serienoptionen. Legen Sie in unserem Fall die X-Achse für das Q-Q-Diagramm auf „Prognostizierte z-Werte“ oder auf „Prognostizierte kumulierte Normalwahrscheinlichkeit“ für das P-P-Diagramm. Entfernen Sie sie dann aus der Reihe, indem Sie auf drei Punkte an der Seite und dann auf Entfernen klicken. Die Einstellungen für das Q-Q-Diagramm sind in der folgenden Abbildung dargestellt:

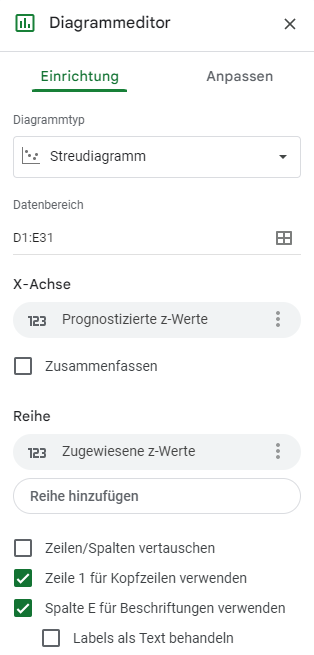
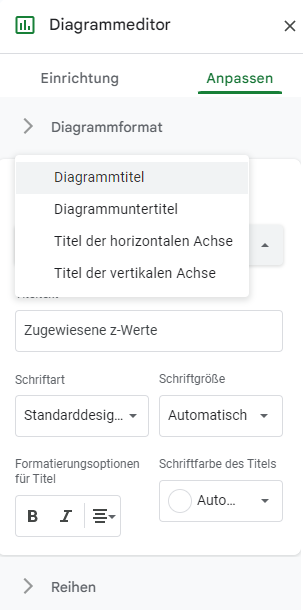
Auf der Registerkarte Anpassen legen Sie den Diagrammtitel, den Titel der horizontalen Achse und den Titel der vertikalen Achse unter der Option Diagrammformat fest:

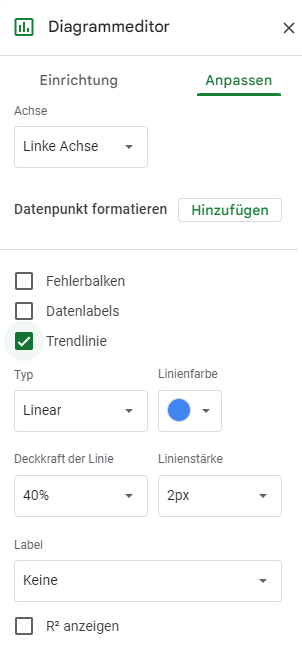
Aktivieren Sie das Kontrollkästchen Trendlinie unter der Option Datenpunkt formatieren:

Und wir haben die folgende Ausgabe: