Exponentieller gleitender (rollender) Mittelwert – Excel & GS
In diesem Tutorial zeigen wir Ihnen, wie Sie den Exponentiellen Gleitenden Mittelwert (Engl. Exponential Moving Average, EMA) in Excel und Google Sheets berechnen können.
Der gleitende (rollende oder laufende) Mittelwert ist eine Reihe von Durchschnittswerten, die die Mittelwerte verschiedener fester Teilmengen des gesamten Datensatzes anzeigen. Ein gleitender 5-Tages-Mittelwert zeigt zum Beispiel den Durchschnitt der letzten 5 Tage an. Der gleitende Mittelwert wird in der Analyse von Zeitreihendaten verwendet, um kurzfristige Schwankungen in einem Datensatz zu glätten und so längerfristige Trends oder Zyklen hervorzuheben und vorherzusagen. Der gleitende Mittelwert kann als einfacher, gewichteter oder exponentieller gleitender Mittelwert berechnet werden.
Der exponentielle gleitende Mittelwert berechnet den gleitenden Durchschnitt einer Teilmenge von Datenpunkten, wobei jedem Datenpunkt eine exponentiell abnehmende Gewichtung zugewiesen wird, je weiter sich die Datenpunkte vom aktuellen Wert entfernen. In diesem Artikel werden wir uns ansehen, wie der exponentielle gleitende Mittelwert berechnet wird.
Formel des exponentiellen gleitenden Mittelwerts
Der exponentielle gleitende Mittelwert für k Datenpunkte (EMAk ) wird mit der folgenden Formel berechnet:
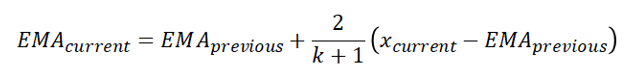
wobei:
xcurrent = der aktuelle Datenwert,
EMAcurrent und EMAprevious = der aktuelle und der vorherige exponentiell gleitende Mittelwert und
k = die gewünschte Anzahl von Perioden.
Den exponentiell gleitender Mittelwert in Excel berechnen
Hintergrund: Die Schlusskurse der Aktie von Apple Inc. an der NASDAQ für die sechzehn Handelstage vom 2. bis 23. Mai 2022 sind in der nachstehenden Tabelle aufgeführt. Berechnen Sie den exponentiellen gleitenden 3-Tages- und den 5-Tages-Mittelwert (EMA) für die Aktienkurse.

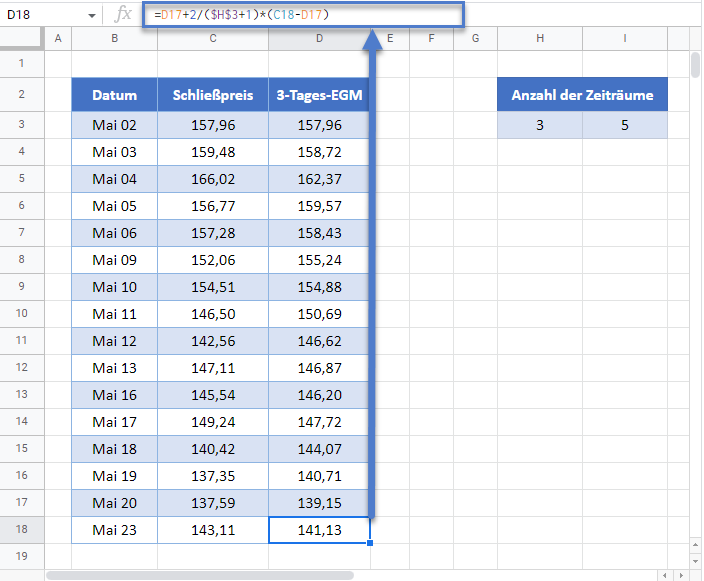
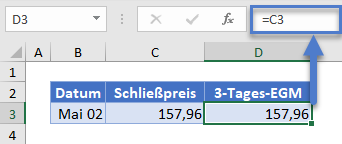
Berechnen Sie den 3-Tages-EMA. Initialisieren Sie den EMA, indem Sie den ersten Wert des Datensatzes als Anfangswert dafür festlegen. Geben Sie also den ersten Schließkurs als ersten EMA ein. Das heißt, der erste Wert des 3-Tages-EMA ist der Schließkurs vom 02. Mai, der 157,96 beträgt.
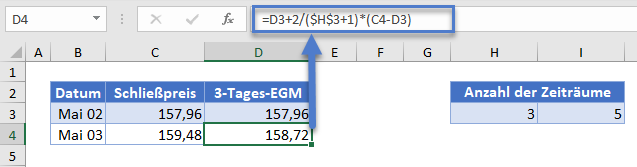
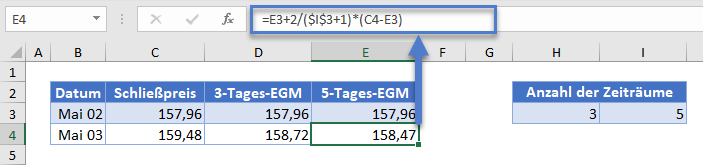
Als Nächstes berechnen Sie die 3-Tages-EMAs anhand der oben genannten Formel und der Anzahl der Zeiträume von 3 Tagen wie in der Abbildung unten dargestellt.
Füllen Sie den Rest der Spalte automatisch aus und Sie erhalten die vollständige 3-Tages-EMA-Spalte wie unten dargestellt.
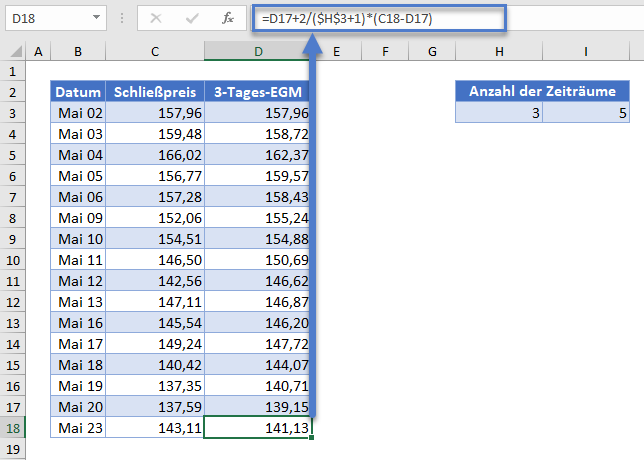
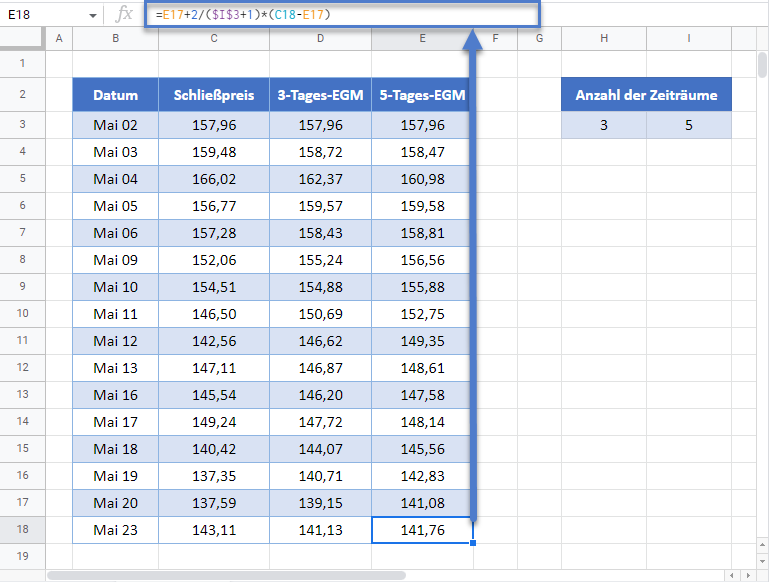
Als Nächstes berechnen Sie den 5-Tages-EMA auf ähnliche Weise wie den 3-Tages-EMA mit dem Unterschied, dass diesmal die Anzahl der Zeiträume 5 Tage beträgt.
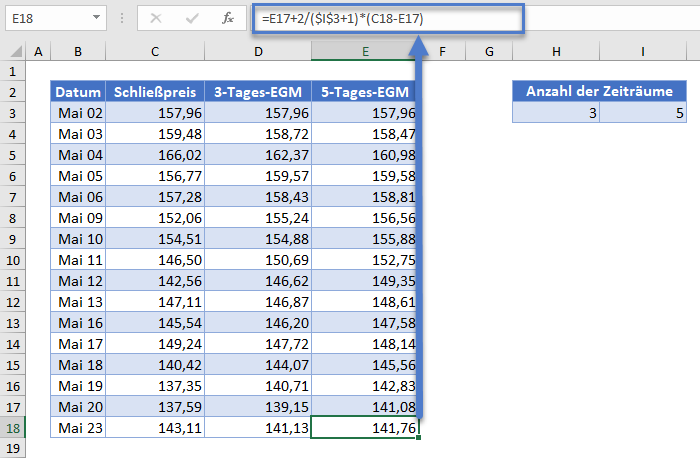
Füllen Sie den Rest der Spalte automatisch aus und Sie haben die vollständige 5-Tages-EMA-Spalte wie unten gezeigt.
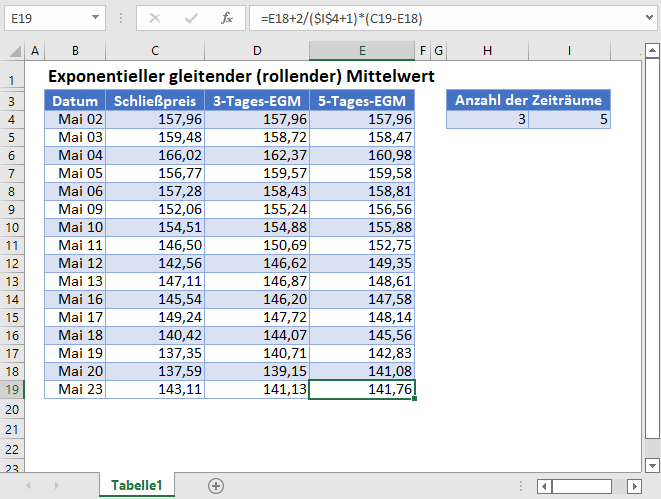
Exponentieller gleitender Mittelwert in Google Sheets
Der exponentielle gleitende Mittelwert kann in Google Sheets wie in den folgenden Abbildungen gezeigt auf ähnliche Weise wie in Excel berechnet werden.