Binomialverteilung in Excel und Google Sheets

In diesem Tutorial zeigen wir Ihnen, wie Sie mit der Binomialverteilung in Excel und Google Sheets arbeiten können.

BINOMVERT-Funktionsübersicht 

Mit der BINOMVERT-Funktion können wir zwei Sachen in Excel berechnen:

1. Die Wahrscheinlichkeit, dass eine bestimmte Anzahl von Binärergebnissen auftritt (z. B. die Wahrscheinlichkeit, dass eine Münze 10 Mal geworfen wird und genau 7 Versuche Kopf ergeben).
2. Die kumulative Wahrscheinlichkeit (z. B. die Wahrscheinlichkeit, dass die Münze zwischen 0 und 7 Mal auf Kopf fällt).

Was ist die Binomialverteilung?

Die Binomialverteilung umfasst den Bereich der Wahrscheinlichkeiten für jedes binäre Ereignis, das sich im Laufe der Zeit wiederholt. Nehmen wir zum Beispiel an, Sie werfen 10 Mal eine Münze. Sicherlich „erwarten“ Sie, dass 5 Mal Kopf und 5 Mal Zahl fällt, aber es kann auch sein, dass Sie am Ende 7 Mal Kopf und 3 Mal Zahl haben. Die Binomialverteilung ermöglicht es uns, die genauen Wahrscheinlichkeiten dieser verschiedenen Ereignisse sowie die Gesamtverteilung der Wahrscheinlichkeit für verschiedene Kombinationen zu messen.

Die Wahrscheinlichkeit jeder einzelnen Anzahl von Erfolgen innerhalb der Binomialverteilung (auch bekannt als Bernoulli-Versuch) lautet wie folgt:

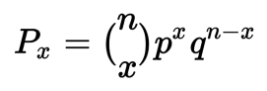
Wobei:

n = die Anzahl der Versuche

x = die Anzahl der „Erfolge“

p = die Erfolgswahrscheinlichkeit für jeden einzelnen Versuch

q = die Misserfolgswahrscheinlichkeit für jeden einzelnen Versuch (auch als 1-p bezeichnet).

Binomialverteilung – Beispiel

Im obigen Beispiel, in dem es darum geht, die Wahrscheinlichkeit zu ermitteln, dass es sich bei 7 von 10 Mal Werfen einer fairen Münze Kopf ergibt, können Sie die folgenden Werte einsetzen:

n = 10
x = 7
p = 0,5
q = 0,5

Nach dem Lösen erhält man eine Wahrscheinlichkeit von 0,1172 (11,72 %), dass genau 7 der 10 Würfe Kopf ergeben.

Binomialverteilung – Excel-Beispiele

Um die individuellen und kumulativen Wahrscheinlichkeiten in Excel zu ermitteln, verwenden wir die BINOMVERT-Funktion. Im obigen Beispiel mit 7 von 10 Münzen, die Kopf ergeben, würde die Excel-Formel wie folgt lauten:

=BINOMVERT(B3;C3;D3; FALSCH)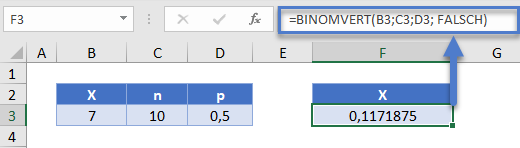

Wobei:

1. Das erste Argument (7) x ist
2. das zweite Argument (10) n ist
3. Das dritte Argument (½) p ist
4. Das vierte Argument FALSCH ist. Wenn es WAHR ist, lässt Excel die kumulative Wahrscheinlichkeit für alle Werte kleiner oder gleich x berechnen.

Tabelle und Diagramm zur Binomialverteilung

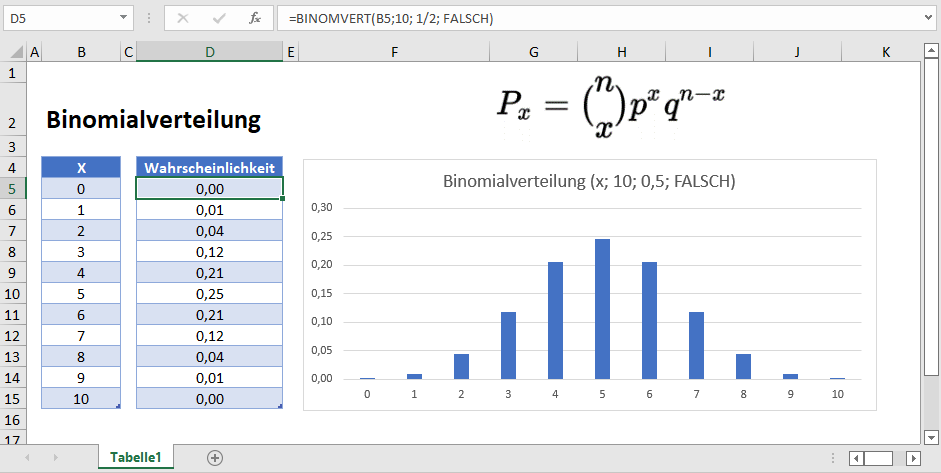
Als Nächstes erstellen wir eine Wahrscheinlichkeitsverteilungstabelle in Excel. Die Wahrscheinlichkeitsverteilung berechnet die Wahrscheinlichkeit für jede Anzahl von Vorkommen.

=BINOMVERT(B10;10; 1/2; FALSCH)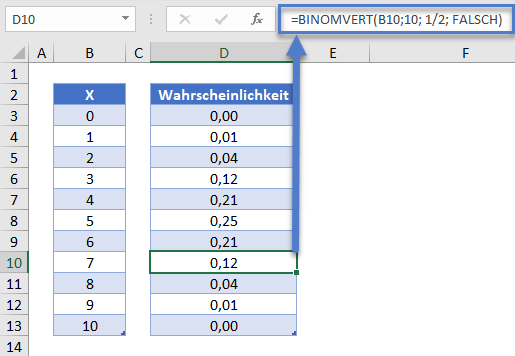

Wie Sie in dieser Tabelle lesen können, ergibt sich eine Wahrscheinlichkeit von 12 %, dass genau 7 von 10 Münzen Kopf ergeben.

Wir können ein Diagramm aus der obigen Binomialwahrscheinlichkeitsverteilungstabelle erstellen.

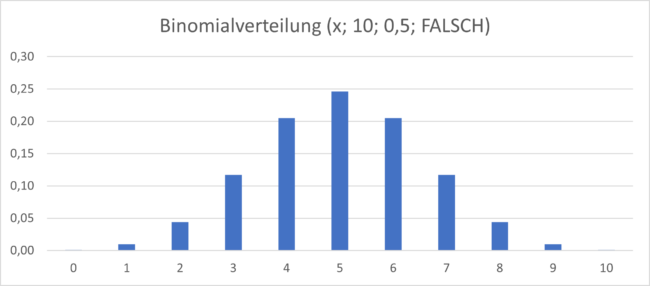
Beachten Sie, dass die Binomialverteilung für dieses Experiment bei x=5 ihren Höhepunkt erreicht. Das liegt daran, dass die erwartete Anzahl von Köpfen beim 10-maligen Werfen einer fairen Münze 5 ist.

Kumulative Binomialwahrscheinlichkeitsverteilung

Alternativ können Sie sich auch auf die kumulative Wahrscheinlichkeitsverteilung konzentrieren. Diese misst die Wahrscheinlichkeit einer Anzahl von Erfolgen, die kleiner oder gleich einer bestimmten Zahl ist.

In grafischer Form sieht sie folgendermaßen aus:

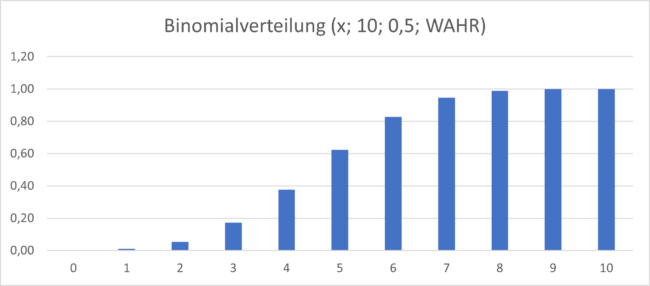
Um die kumulative Wahrscheinlichkeit zu berechnen, können Sie einfach die im vorherigen Abschnitt berechneten Einzelwahrscheinlichkeiten summieren.

Oder Sie können die BINOMVERT-Funktion wie folgt verwenden:

=BINOMVERT(B10;10; 1/2; WAHR)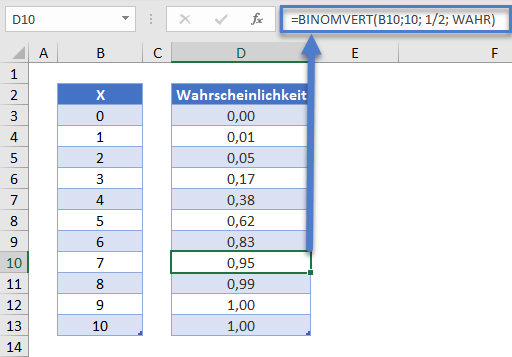

Beachten Sie, dass wir zur Berechnung der kumulativen Wahrscheinlichkeit das letzte Argument auf WAHR statt auf FALSCH setzen.

Mathematisch lässt sich diese Formel folgendermaßen ausdrücken: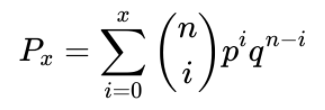

BINOM.VERT.BEREICH – Wahrscheinlichkeit eines Wertebereichs ermitteln

Während BIMOMVERT dazu dient, die Wahrscheinlichkeit eines einzelnen diskreten Punktes zu ermitteln, ermöglicht die Funktion BINOM.VERT.BEREICH die Ermittlung der Wahrscheinlichkeit, einen bestimmten Bereich von Erfolgen zu erreichen.

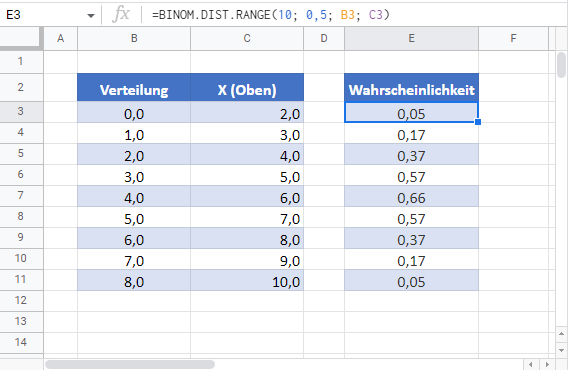
Anhand des Kopf-oder-Zahl-Beispiels können wir mit der folgenden Formel die Wahrscheinlichkeit ermitteln, dass zwischen 6 und 8 unserer 10 Versuche Kopf ergeben.

=BINOM.VERT.BEREICH(10; 0,5; B9; C9)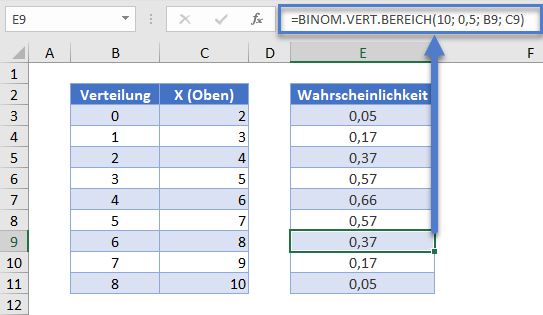

Binomialerwartungswert – E(x)

Für eine Binomialverteilung mit einer Anzahl von n Bernoulli-Versuchen können wir den Erwartungswert für die Anzahl der Erfolge folgendermaßen ausdrücken:

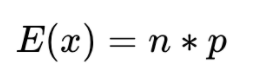
Dieser kann in Excel wie folgt berechnet werden:

=B6*C6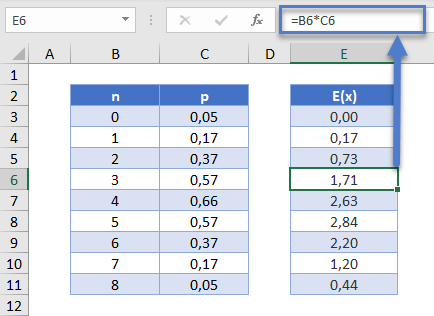

Binomialvarianz – Var(x)

Um die Varianz der Verteilung zu berechnen, verwenden Sie die folgende Formel: 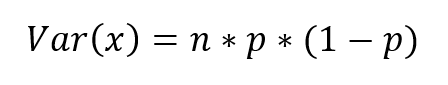Diese kann in Excel wie folgt berechnet werden:

=B6*C6*(1-C6)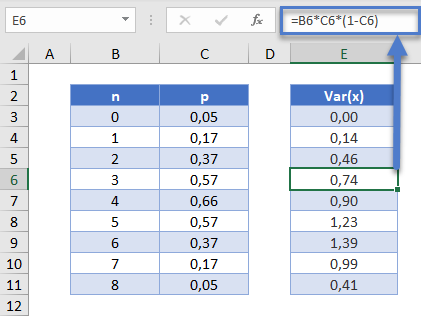

 

Binomialverteilung in Google Sheets

Ähnlich wie in Excel können Sie die Binomialverteilung auch in Google Sheets berechnen.

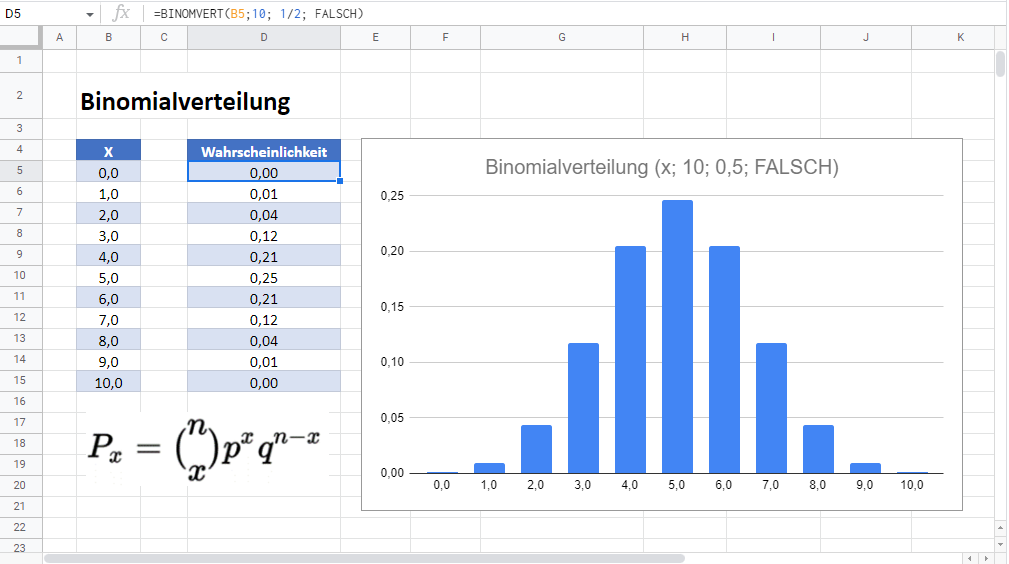
Hinweis: Die Excel-Funktion BINOM.VERT.BEREICH behält ihre englische Bezeichnung (BINOM.DIST.RANGE) auch in der deutschsprachigen Version von Google Sheets bei.