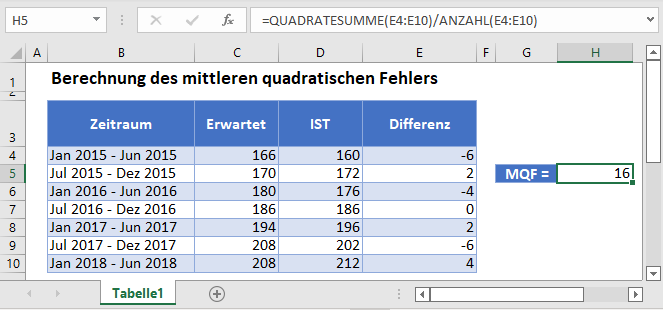
Der mittlere quadratische Fehler (MQF oder Engl. MSE) ist eine Schätzung, die die durchschnittliche quadrierte Differenz zwischen den geschätzten und den tatsächlichen Werten einer Datenverteilung misst. Bei der Regressionsanalyse berechnet der MQF die durchschnittlichen quadrierten Differenzen zwischen den Punkten und der Regressionslinie. Das heißt, der Mittelwert der Quadrate der Residuen.

Der MQF ist immer positiv und nimmt in dem Maße ab, wie der Fehler in den Prognosen abnimmt. Das heißt, je näher die vorhergesagten Werte an den tatsächlichen Werten liegen, desto geringer ist der MQF.

Der MQF einer Reihe von Beobachtungen wird mit der folgenden Formel berechnet:

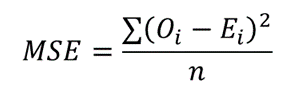
wobei:

Oi = die beobachteten Werte.

Ei = die erwarteten Werte.

∑ = ein griechischer Buchstabe namens Sigma, der für „Summe“ steht.

n = der Stichprobenumfang (die Anzahl der Beobachtungen).

Den Mittleren Quadratischen Fehler in Excel berechnen

Beispiel

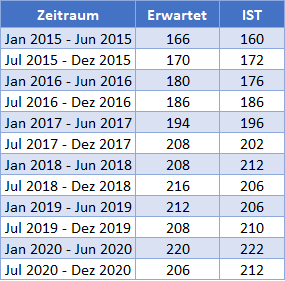
Hintergrund: Die nachstehende Tabelle zeigt die halbjährlich erwarteten und die tatsächlichen Ausgaben in Tausend Dollar für den Wohn- und Nichtwohngebäudebau in einem bestimmten Bundesstaat der Vereinigten Staaten von Januar 2015 bis Juli 2020.

Berechnen Sie anhand der Daten in der Tabelle den mittleren quadratischen Fehler (MQF) zwischen den tatsächlichen und den prognostizierten Daten.

 

Verwendung der QUADRATESUMME-Funktion

Ermitteln Sie zunächst die Differenz zwischen den vorhergesagten und den tatsächlichen Werten wie in der folgenden Abbildung dargestellt.

=C2-B2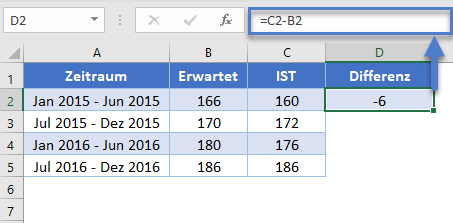

Ergänzen Sie den Rest der Spalte wie in der folgenden Abbildung gezeigt.

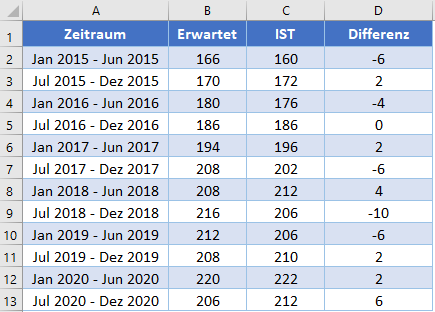
Berechnen Sie anschließend den MQF mit der QUADRATESUMME-Funktion wie in der folgenden Abbildung dargestellt.

 

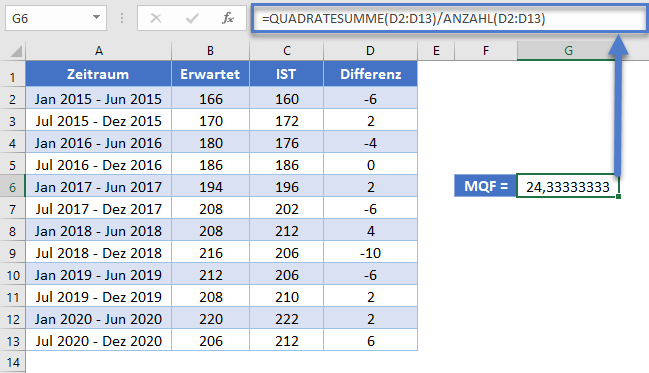
Verwendung der MITTELWERT-Funktion

Eine weitere Methode, die Sie einsetzen können, um den MQF eines Datensatzes zu erhalten, ist die Verwendung der MITTELWERT-Funktion. Diese Methode wird im Folgenden beschrieben.

Führen Sie zunächst die Schritte aus, die in der oben beschriebenen Methode der QUADRATESUMME-Funktion beschrieben sind, um die Differenz zwischen den vorhergesagten und den tatsächlichen Werten wie in der folgenden Abbildung dargestellt zu erhalten.

=C2-B2

Berechnen Sie anschließend das Quadrat der Differenzen zwischen den tatsächlichen und den vorhergesagten Werten wie in der folgenden Abbildung dargestellt.

=D2^2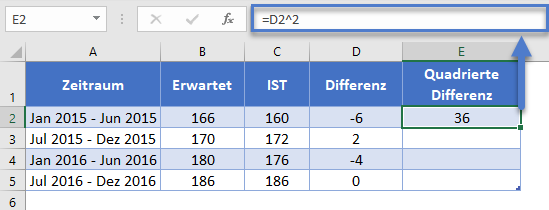

Ergänzen Sie den Rest der Spalten wie in der folgenden Abbildung gezeigt.

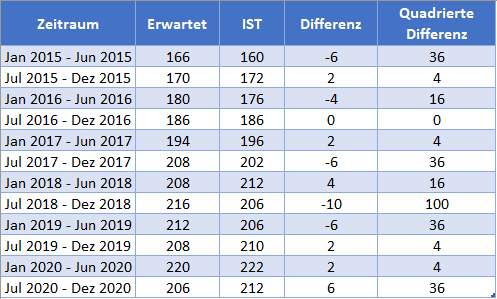
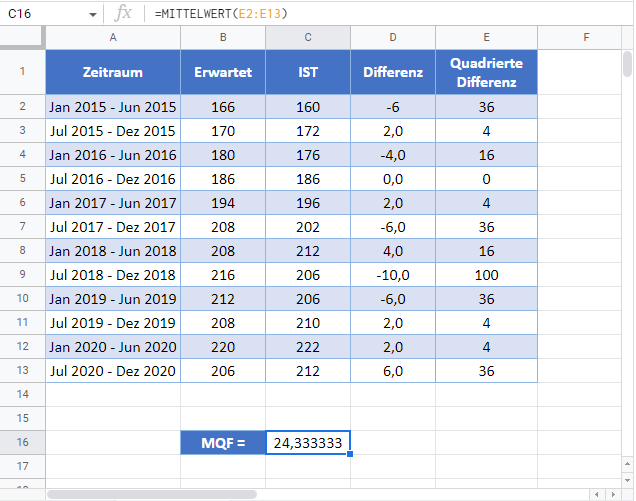
Berechnen Sie anschließend den MQF, indem Sie den Mittelwert der Spalte „Quadrierte Differenzen“ wie in der folgenden Abbildung dargestellt bilden.

=MITTELWERT(E2:E13)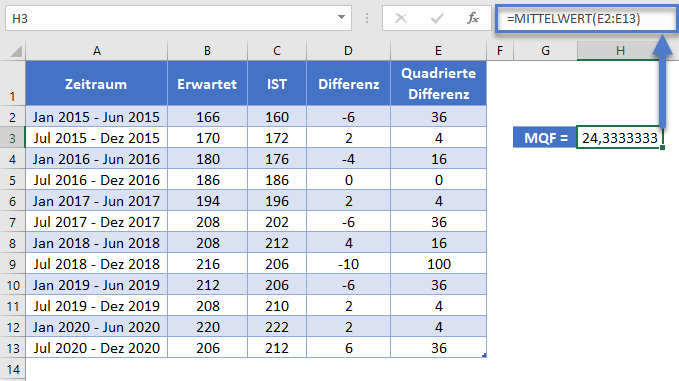

 

Verwendung der MQF-Formel

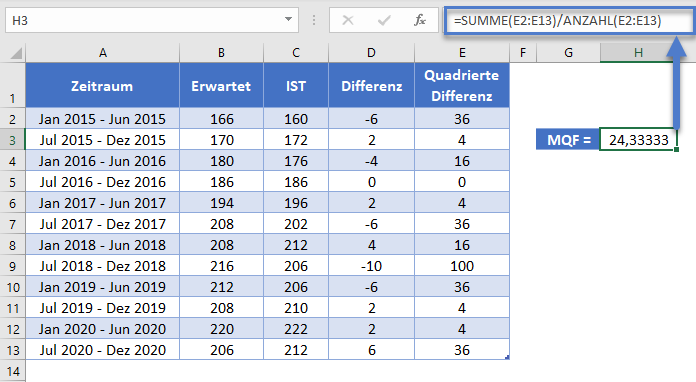
Eine weitere Methode zur Ermittlung vom MQF eines Datensatzes ist die Verwendung der MQF-Formel. Dazu wird die Summe der quadrierten Differenzen gebildet und das Ergebnis durch die Anzahl (Stichprobengröße) wie in der folgenden Abbildung dargestellt geteilt.

=SUMME(E2:E13)/ANZAHL(E2:E13)

 

Mittlerer quadratischer Fehler in Google Sheets

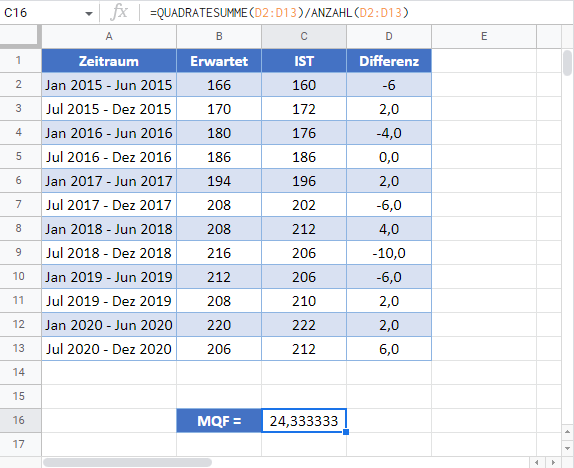
Der mittlere quadratische Fehler (MQF) kann in Google Sheets wie in den folgenden Abbildungen gezeigt auf genau dieselbe Weise wie in Excel berechnet werden.

Verwendung der QUADRATESUMME-Funktion

Verwendung der MITTELWERT-Funktion